Stable Distributions
2. Parameterisation of stable
distributions
[this page | pdf | references | back links]
Return
to Abstract and Contents
Next
page
2.1 As noted in Section 1 any
specific stable distributional form is characterised by four parameters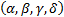 
.
Nolan (2005)
notes that there are multiple definitions used in the literature regarding what
these parameters mean. He focuses there on two, which he denotes by 
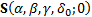and
,
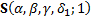that are differentiated according to the meaning given to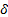 
. The
first is the one that he concentrates on, because it has better numerical
behaviour and intuitive meaning, but the second is more commonly used in the
literature. We call the former the ‘0-parameterisation’ and the latter the
‘1-parameterisation’ in these pages.
2.2 In
either of these descriptions:
(a)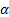 
is the index
of the distribution, also known as the index of stability or characteristic
exponent, and must be in the range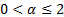 
.
The constant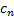 
in
the formula in Section
1.3 must be of the form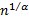 
;
(b)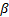 
is the skewness
of the distribution and must be in the range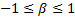 
. If 
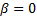then
the distribution is symmetric, if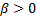 
then it is skewed to the
right and if 
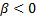then it is skewed to the
left;
(c)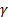 
is a
scale parameter and can be any positive number; and
(d) 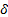is a
location parameter, shifting the distribution right if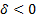 
and
left if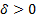 
.
2.3In either description, the distributional form is
normally defined via the distribution’s characteristic function, i.e. the
(complex) function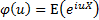 
,
where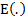 
is
the expectation operator. Nolan (2005) uses the following definitions:
(a) A random
variable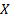 
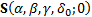is if
it has characteristic function
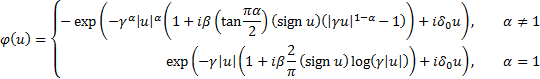
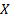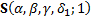(b) A random variable is if
it has characteristic function
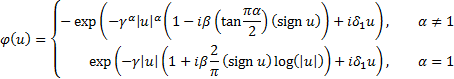
2.4 The
location parameters are related by:
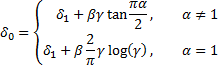
or
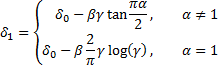
2.5 Nolan (2005)
notes that if 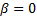then the
0-parameterisation and the 1-parameterisation coincide. When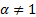 
and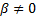 
then
the parameterisations differ by a shift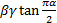 
which
gets infinitely large as 
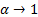. Nolan argues that the
0-parameterisation is a better approach because it is jointly continuous in all
four parameters, but accepts that the 1-parameterisation is simpler
algebraically, so is unlikely to disappear from the literature.
NAVIGATION LINKS
Contents | Prev | Next