Stable Distributions
1. Introduction
[this page | pdf | references | back links]
Return
to Abstract and Contents
Next
page
1.1 Stable distributions are a class of probability
distributions that have interesting theoretical and practical properties that
make them potentially useful for modelling financial data. In a sense that we
will explore further below, they generalise the Normal distribution. They also
allow fat tails and skewness, characteristics that are also frequently observed
in financial data. Traditionally they have been perceived to be subject to the
practical disadvantage that they have infinite variances (apart from the
special case of the Normal distribution) and thus are not particularly easy to
manipulate mathematically. However, more recently, mathematical tools and
programs have been developed that simplify such manipulations.
1.2 Whether stable distributions are actually good
at modelling financial data is not something that we explore in depth in these
pages. Longuin
(1993), when analysing the distribution of U.S. equity returns, concluded
that their distribution was not sufficiently fat-tailed to be adequately
modelled by Levy stable distributions, even if it was fatter tailed than
implied by the normal distribution. Moreover, implicit within the theoretical
justification for (non-Normal) stable distributions in such a context is an
assumption that aggregate returns arise from the combined impact of a large
number of smaller independent innovations, so that a generalisation of the
Central Limit Theorem applies, see Section 4.
Fat-tailed behaviour in the distribution of aggregate returns in line with
stable laws can then be expected to arise if it is assumed that each of these
smaller innovations is also (suitably) fat-tailed. The challenge is that this
is not necessarily how fat tails arise in aggregate return data. Fat tails may
instead arise partly or wholly due to distributional mixtures, e.g. regime
shifts or time-varying volatility, or from one-off (systemic) ‘shocks’ that
cannot be conceptually decomposed in to lots of smaller independent elements,
see e.g. Kemp
(2009). The latter might include the impact of an aggregate loss of risk
appetite (and feedback effects that might then arise because of changed
perceptions amongst market participants regarding the views of others).
1.3 The implicit assumption underlying stable
distributions referred to in the previous paragraph is revealed by their
defining characteristic, and the reason for the term stable, which is
that they retain their shape (suitably scaled and shifted) under addition. The
definition of a stable distribution is that if 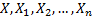 are
independent, identically distributed random variables coming from such a distribution,
then for every
are
independent, identically distributed random variables coming from such a distribution,
then for every 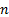 we have the following
relationship for some constants
we have the following
relationship for some constants 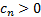 and
and
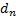 :
:
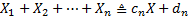
Here 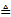 means equality in
distributional form, i.e. the left and right hand sides have the same
probability distribution. The distribution is called strictly stable if
means equality in
distributional form, i.e. the left and right hand sides have the same
probability distribution. The distribution is called strictly stable if 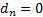 for
all
for
all 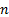 . Some authors use the
term sum stable to differentiate from other types of stability that
might apply.
. Some authors use the
term sum stable to differentiate from other types of stability that
might apply.
1.4 Normal distributions satisfy this property,
indeed they are the only distributions with finite variance that do so. Other
probability distributions that exhibit the stability property described above
include the Cauchy distribution and the Levy distribution.
1.5 The class of all distributions that satisfy the
above property is described by four parameters, 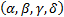 .
In general there are no simple closed form formulae for the probability
densities,
.
In general there are no simple closed form formulae for the probability
densities, 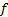 , and cumulative
distribution functions,
, and cumulative
distribution functions, 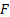 , applicable to these
distributional forms (exceptions are the normal, Cauchy and Levy distributions),
but there are now reliable computer algorithms for working with them.
, applicable to these
distributional forms (exceptions are the normal, Cauchy and Levy distributions),
but there are now reliable computer algorithms for working with them.
NAVIGATION LINKS
Contents | Prev | Next