Marginal Tail Value-at-Risk (Marginal
TVaR)
[this page | pdf | back links]
Suppose we have a set of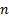 
risk
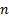factors which we can characterise by an -dimensional
vector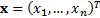 
.
Suppose that the (active) exposures we have to these factors are characterised
by another 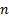-dimensional vector, 
.
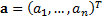Then the aggregate exposure is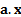 
.
The Value-at-Risk of the portfolio of exposures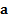 
at
confidence level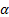 
, 
,
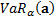is usually defined to be the value such that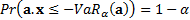 
.
The Tail Value-at-Risk is defined as:
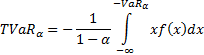
The Marginal Tail Value-at-Risk,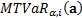 
,
is the sensitivity of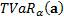 
to
a small change in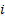 
’th exposure. It is therefore:
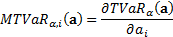
Because Tail Value-at-Risk is (first-order) homogeneous (for
a continuous probability distribution) it satisfies the Euler capital
allocation principle and hence:
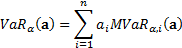
If the risk factors are multivariate normally distributed
then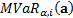 
can
be expressed using a relatively simple formula, see here.