Marginal Tail Value-at-Risk (Marginal
TVaR) when underlying distribution is multivariate normal
[this page | pdf | back links]
Suppose we have a set of 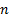 risk factors
which we can characterise by an
risk factors
which we can characterise by an 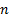 -dimensional
vector
-dimensional
vector 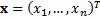 . Suppose that
the (active) exposures we have to these factors are characterised by another
. Suppose that
the (active) exposures we have to these factors are characterised by another 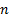 -dimensional
vector,
-dimensional
vector, 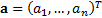 . The aggregate
exposure is then
. The aggregate
exposure is then 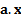 .
.
The Value-at-Risk, 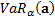 , of the
portfolio of exposures
, of the
portfolio of exposures 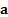 at confidence
level
at confidence
level 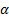 , is defined as
the
, is defined as
the
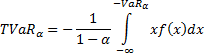
The Marginal Tail Value-at-Risk, 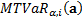 , is the
sensitivity of
, is the
sensitivity of 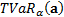 to a small change
in
to a small change
in 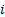 ’th exposure. It
is therefore:
’th exposure. It
is therefore:
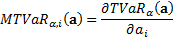
In the case where the risk factors are multivariate normally
distributed with mean 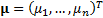 and covariance
matrix
and covariance
matrix 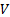 whose elements
are
whose elements
are 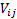 we have
we have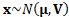 and hence
and hence 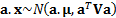 . Hence
. Hence 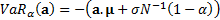 .
.
Given the formula for the truncated first moments of a normal distribution
we have:
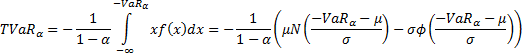
where 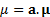 ,
, 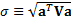 ,
, 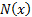 is the
(standard) normal cumulative distribution function and
is the
(standard) normal cumulative distribution function and 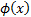 is the
(standard) normal probability density function.
is the
(standard) normal probability density function.
Hence:
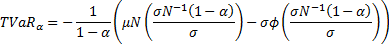
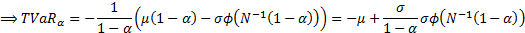
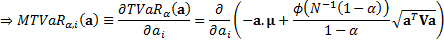
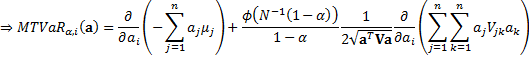
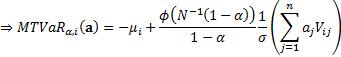
The second of these terms can be expressed in terms of the
correlation between 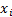 and
and 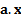 in a manner
similar to Marginal
VaR when underlying distribution is multivariate normal.
in a manner
similar to Marginal
VaR when underlying distribution is multivariate normal.
As risks arising from individual positions interact there is
no universally agreed way of subdividing the overall risk into contributions
from individual positions. However, a commonly used way is to define the Contribution
to Tail Value-at-Risk, 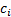 , of the
, of the 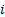 ’th
position,
’th
position, 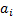 to be as
follows:
to be as
follows:
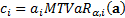
Conveniently the 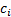 then sum to the
overall VaR:
then sum to the
overall VaR:
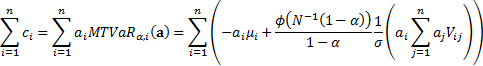
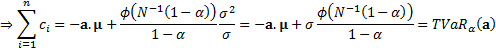
The property that the contributions to risk add to the total
risk is a generic feature of any risk measure that is (first-order)
homogeneous, a property that Tail Value-at-Risk exhibits.