Enterprise Risk Management Formula Book
12. Copulas
[this page | pdf | back links]
12.1 Definition
A copula
is a multivariate cumulative distribution function for an 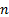 dimensional
random vector
dimensional
random vector 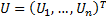 in the unit hypercube (
in the unit hypercube (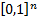 ) that has uniform
marginals,
) that has uniform
marginals, 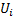 , each distributed
according to
, each distributed
according to 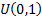 but not in general
independent of each other. Let
but not in general
independent of each other. Let 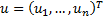 also be restricted to
the unit hypercube
also be restricted to
the unit hypercube 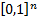 . Then a copula is
defined as a function of the form:
. Then a copula is
defined as a function of the form:
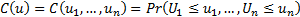
Equivalently 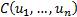 is the joint cumulative
distribution function for the random vector
is the joint cumulative
distribution function for the random vector 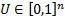 .
.
The copula density (for a continuous copula) is the
pdf for which the cdf is the copula.
12.2 Properties
In the bivariate case (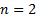 ) for a general function
) for a general function 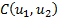 to be a copula it must
satisfy the following properties:
to be a copula it must
satisfy the following properties:
1. 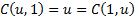 for all
for all 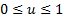
2. 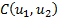 must be increasing in
both
must be increasing in
both 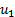 and
and 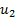
3. 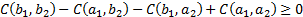 for all
for all 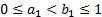 and
and 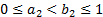
4. 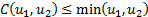
5. 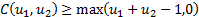
12.3 Sklar’s theorem
If 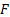 is a joint (cumulative)
distribution with marginal cdf’s
is a joint (cumulative)
distribution with marginal cdf’s 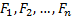 then there exists a
copula
then there exists a
copula 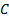 which maps the unit
hypercube
which maps the unit
hypercube 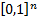 onto the interval
onto the interval 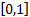 such that for all
such that for all 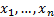 we have:
we have:
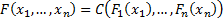
Moreover, if the 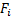 are continuous functions
then the copula is unique and
are continuous functions
then the copula is unique and
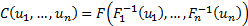
Conversely, suppose 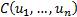 is a copula and
is a copula and 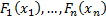 are univariate cdf’s.
Then the function
are univariate cdf’s.
Then the function 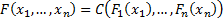 is a joint distribution
function with marginal cdf’s
is a joint distribution
function with marginal cdf’s 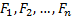 .
.
12.4 Example copulas
The Archimedean family
involves copulas of the following form, where 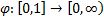 ,
, 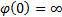 ,
, 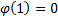 ,
, 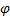 is
continuous and strictly decreasing and
is
continuous and strictly decreasing and 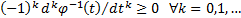
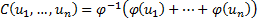
Special cases include the Clayton copula which has
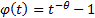 (for some suitable value
of
(for some suitable value
of 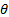 ) and the independence or
product copula which has
) and the independence or
product copula which has 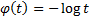 .
.
12.5 Tail dependence
If 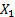 and
and 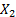 are continuous random
variables with copula
are continuous random
variables with copula 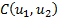 then their coefficient
of (joint lower) tail dependence (if it exists) is:
then their coefficient
of (joint lower) tail dependence (if it exists) is:
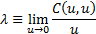
For continuous random variables 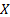 and
and 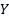 each
with lower limit of
each
with lower limit of 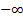 the coefficient of
(lower) tail dependence is also:
the coefficient of
(lower) tail dependence is also:
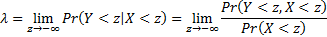
12.6 Simulating copulas
Correlated Gaussian (i.e. multivariate normal) random
variables (i.e. random variables with a Gaussian copula and Gaussian marginals)
can be generated using Cholesky
decomposition.
For random variables that have a Gaussian copula but
non-normal marginal (with cdfs 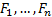 ) we can generate a
vector
) we can generate a
vector 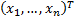 of correlated Gaussian
random variables as above and then transform as per
of correlated Gaussian
random variables as above and then transform as per 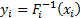 .
.
In general, for non-Gaussian copulas we may need to generate
a vector of unit uniform random variables 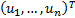 and then transform them
using
and then transform them
using 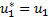 ,
, 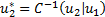 etc.
etc.
NAVIGATION LINKS
Contents | Prev | Next