Enterprise Risk Management Formula Book
11. Extreme value theory
[this page | pdf | back links]
See also here.
11.1 Maximum domain of attraction (MDA)
Suppose that i.i.d. random variables 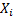 have cdf
have cdf 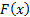 . Suppose also
that there exist sequences
. Suppose also
that there exist sequences 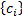 and
and 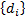 and a cdf
and a cdf 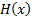 such that:
such that:
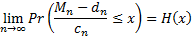
where 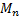 is the random
variable corresponding to the block maximum for blocks of such variables of
length
is the random
variable corresponding to the block maximum for blocks of such variables of
length 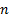 , i.e. each
(independent) realisation of the series
, i.e. each
(independent) realisation of the series 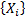 is used to
create a realisation of
is used to
create a realisation of 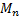 given by
given by 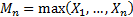 .
.
Then 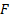 is said to be
in the maximum domain of attraction (MDA) of
is said to be
in the maximum domain of attraction (MDA) of 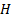 ,
written
,
written 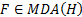
11.2 Fisher-Tippett theorem
If 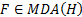 where
where 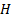 is
a non-degenerate cdf then
is
a non-degenerate cdf then 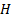 must be a
Generalised Extreme Value (GEV) distribution.
must be a
Generalised Extreme Value (GEV) distribution.
If 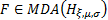 where
where 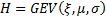 then by
replacing
then by
replacing 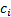 by
by 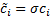 and
and 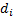 by
by 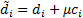 we see that
we see that 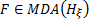 where
where 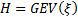 .
.
11.3 The Pickands-Balkema-de Haan (PBH) theorem
Let 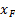 be the
maximum limiting value of the random variable
be the
maximum limiting value of the random variable 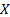 .
Then the PBH theorem states that we can find a function
.
Then the PBH theorem states that we can find a function 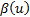 such that
such that
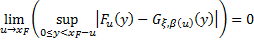
if and only if that 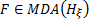
11.4 Estimating tail distributions
Suppose that the underlying loss distribution is in the
maximum domain of attraction of the Frechét distribution and it has a tail of
the form: 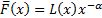 for some
slowly varying
for some
slowly varying 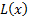 , where
, where 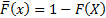 . Then the
Hill estimator for the (upper) tail index, given
. Then the
Hill estimator for the (upper) tail index, given 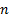 ordered
observations,
ordered
observations, 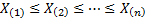 , assuming
that the (upper) tail contains
, assuming
that the (upper) tail contains 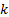 entries is:
entries is:
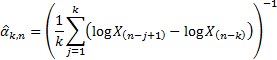
NAVIGATION LINKS
Contents | Prev | Next