Enterprise Risk Management Formula Book
Appendix A.2: Probability Distributions:
Continuous (univariate) distributions (b) exponential, F, generalised extreme
value (GEV) (and Frechét, Gumbel and Weibull)
[this page | pdf]
Distribution name
Exponential
distribution
|
|
Common notation
|
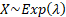
|
|
Parameters
|
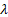 = inverse
scale (i.e. rate) parameter ( = inverse
scale (i.e. rate) parameter (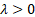 ) )
|
|
Domain
|
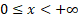
|
|
Probability density
function
|
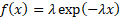
|
|
Cumulative distribution
function
|
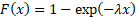
|
|
Mean
|

|
|
Variance
|
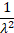
|
|
Skewness
|
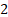
|
|
(Excess) kurtosis
|
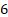
|
|
Characteristic function
|
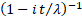
|
|
Other comments
|
Also called the negative exponential distribution.
The mode of an exponential distribution is 0. The exponential distribution
describes the time between events if these events follow a Poisson process.
It is not the same as the exponential family of distributions. The quantile
function, i.e. the inverse cumulative distribution function, is 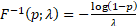 . .
The non-central moments (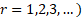 are are
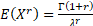 . Its
median is . Its
median is 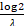 . .
|
|
Distribution name
|
F distribution
|
|
Common notation
|
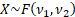
|
|
Parameters
|
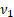 = degrees
of freedom (first) (positive integer) = degrees
of freedom (first) (positive integer)
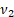 = degrees
of freedom (second) (positive integer) = degrees
of freedom (second) (positive integer)
|
|
Domain
|
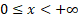
|
|
Probability density
function
|
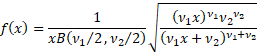
|
|
Cumulative distribution
function
|
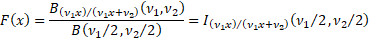
|
|
Mean
|

|
|
Variance
|
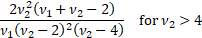
|
|
Skewness
|
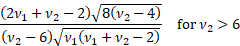
|
|
(Excess) kurtosis
|
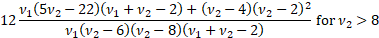
|
|
Characteristic function
|
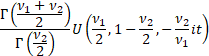
Where 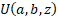 is the
confluent hypergeometric function of the second kind is the
confluent hypergeometric function of the second kind
|
|
Other comments
|
The F distribution is a special case of the Pearson
type 6 distribution. It is also known as Snedecor’s F or the
Fisher-Snedecor distribution. It commonly arises in statistical tests linked
to analysis of variance.
If 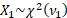 and and 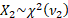 are
independent random variables then are
independent random variables then
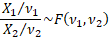
The F-distribution is a particular example of the
beta prime distribution.
The mode is 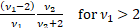 . There is
no simple closed form for the median. . There is
no simple closed form for the median.
|
|
Distribution name
|
Generalised extreme
value (GEV) distribution (for maxima)
|
|
Common notation
|
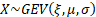
|
|
Parameters
|
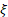 = shape
parameter = shape
parameter
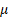 = location
parameter = location
parameter
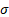 = scale
parameter = scale
parameter
|
|
Domain
|
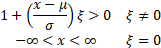
|
|
Probability density
function
|
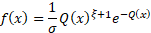
where
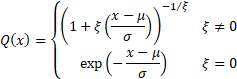
|
|
Cumulative distribution
function
|
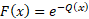
|
|
Mean
|
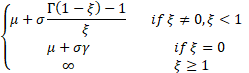
where 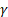 is Euler’s
constant, i.e. is Euler’s
constant, i.e. 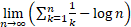
|
|
Variance
|
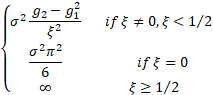
Where 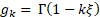
|
|
Skewness
|
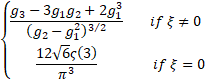
where 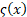 is the
Riemann zeta function, i.e. is the
Riemann zeta function, i.e. 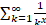 . .
|
|
(Excess) kurtosis
|
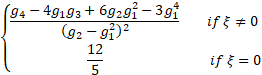
|
|
Other comments
|
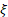 defines
the tail behaviour of the distribution. The sub-families defined by defines
the tail behaviour of the distribution. The sub-families defined by 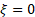 (Type
I), (Type
I), 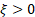 (Type II)
and (Type II)
and 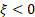 (Type III)
correspond to the Gumbel, Frechét and Weibull families respectively. (Type III)
correspond to the Gumbel, Frechét and Weibull families respectively.
An important special case when analysing threshold
exceedances involves 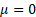 (and
normally (and
normally 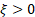 ) and this
special case may be referred to as ) and this
special case may be referred to as 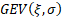 . .
|
NAVIGATION LINKS
Contents | Prev | Next