Enterprise Risk Management Formula Book
Appendix A.2: Probability Distributions:
Continuous (univariate) distributions (c) generalised Pareto, lognormal,
Student’s t
[this page | pdf]
Distribution name
Generalised
Pareto distribution (GPD)
|
|
Common notation
|
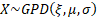
|
|
Parameters
|
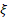 = shape
parameter = shape
parameter
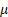 = location
parameter = location
parameter
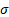 = scale
parameter ( = scale
parameter (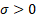 ) )
|
|
Domain
|
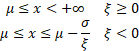
|
|
Probability density
function
|
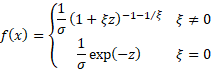
where
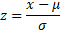
|
|
Cumulative distribution
function
|
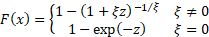
|
|
Mean
|
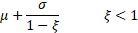
|
|
Variance
|
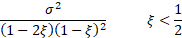
|
|
Skewness
|
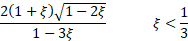
|
|
(Excess) kurtosis
|
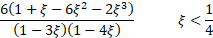
|
|
Other comments
|
GPD is used in the peaks over thresholds variant of
extreme value theory
|
|
Distribution name
|
Lognormal
distribution
|
|
Common notation
|
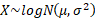
|
|
Parameters
|
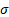 = scale
parameter ( = scale
parameter (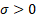 ) )
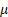 = location
parameter = location
parameter
|
|
Domain
|
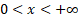
|
|
Probability density
function
|
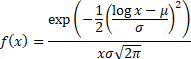
|
|
Cumulative distribution
function
|
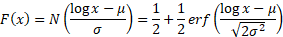
|
|
Mean
|
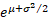
|
|
Variance
|
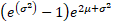
|
|
Skewness
|
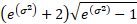
|
|
(Excess) kurtosis
|
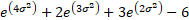
|
|
Characteristic function
|
No simple expression that is not divergent
|
|
Other comments
|
The median of a lognormal distribution is 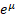 and its
mode is and its
mode is 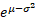 . .
The truncated moments of 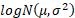 are: are:
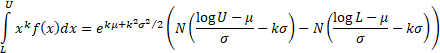
|
|
Distribution name
|
(Standard)
Student’s t distribution
|
|
Common notation
|
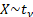
|
|
Parameters
|
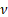 = degrees
of freedom ( = degrees
of freedom (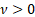 , usually , usually 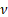 is
an integer although in some situations a non-integral is
an integer although in some situations a non-integral 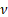 can
arise) can
arise)
|
|
Domain
|
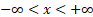
|
|
Probability density
function
|
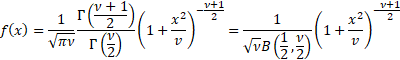
|
|
Cumulative distribution
function
|
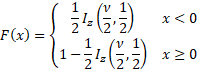
where 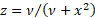
|
|
Mean
|
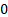
|
|
Variance
|
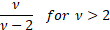
|
|
Skewness
|
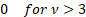
|
|
(Excess) kurtosis
|
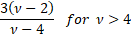
|
|
Characteristic function
|
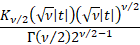
where 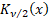 is a
Bessel function is a
Bessel function
|
|
Other comments
|
The Student’s t distribution (more simply the t
distribution) arises when estimating the mean of a normally distributed
population when sample sizes are small and the population standard deviation
is unknown.
It is a special case of the generalised hyperbolic
distribution.
Its non-central moments if  is
even and is
even and 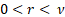 are: are:
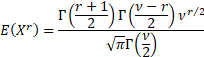
If 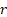 is even
and is even
and 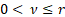 then then 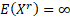 , if , if 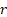 is
odd and is
odd and 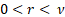 then then 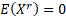 and if and if 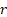 is
odd and is
odd and 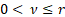 then then 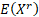 is undefined. is undefined.
|
NAVIGATION LINKS
Contents | Prev | Next