Solar-powered space flight
3c. Power required to reach earth orbit
ignoring atmospheric drag: Assuming that we launch approximately
‘horizontally’, with variable exhaust velocity
[this page | pdf | references | back links]
Return to Abstract
and Contents
Next page
3.8 Better still
is to accelerate horizontally. Indeed, this approach appears to be the optimal
way of reaching orbit. The faster the horizontal speed, the greater the
centrifugal effects offsetting gravity (which of course completely offset the
downward pull of gravity when orbit is reached); the effective downward
acceleration becomes 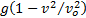 rather than
rather than 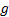 .
We would therefore eject propellant out at an angle that just counteracts this
downward acceleration and we would choose
.
We would therefore eject propellant out at an angle that just counteracts this
downward acceleration and we would choose 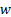 to maximise
to maximise 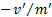 , so:
, so:
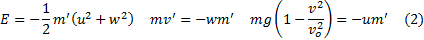
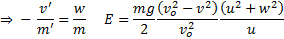
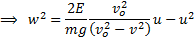

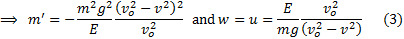
3.9 Flight
metrics for various ratios of 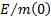 using this approach
are in Table 3 (in theory
using this approach
are in Table 3 (in theory  and
and  would
rise without limit and the vehicle would only asymptotically reach orbit if it
followed these formulae precisely). The maximum acceleration would now be at
the start of the flight, see Figure 3. It is optimal to eject propellant at 45°
to the vertical.
would
rise without limit and the vehicle would only asymptotically reach orbit if it
followed these formulae precisely). The maximum acceleration would now be at
the start of the flight, see Figure 3. It is optimal to eject propellant at 45°
to the vertical.
Table 3. Flight characteristics to reach orbit for a
range of 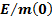 , if propellant is
ejected at optimal speeds and the vehicle accelerates horizontally
, if propellant is
ejected at optimal speeds and the vehicle accelerates horizontally
|
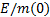 (kW/kg) (kW/kg)
|
Ratio of propellant
to lifted mass
|
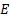 (kW
per kg lifted mass) (kW
per kg lifted mass)
|
Flight time to
reach orbital velocity (s)
|
Maximum
acceleration ms-2
|
|
100
|
0.5
|
152
|
N/A
|
10
|
|
50
|
1.0
|
102
|
N/A
|
10
|
|
30
|
1.7
|
82
|
N/A
|
10
|
|
15
|
3.5
|
67
|
N/A
|
10
|
|
10
|
5.2
|
62
|
N/A
|
10
|
|
8
|
6.5
|
60
|
N/A
|
10
|
|
6
|
8.7
|
58
|
N/A
|
10
|
Figure 3. Plot of vehicle velocity as a function of time,
if vehicle accelerates horizontally and propellant is ejected at optimal speeds
and angles, if 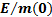 = 10 kW/kg
= 10 kW/kg
NAVIGATION LINKS
Contents | Prev | Next