Quantitative Return Forecasting
4. Generalising linear regression
techniques
[this page | pdf | references | back links]
Return to Abstract and
Contents
Next page
4.1 Multivariate regression involves the
dependent variables (the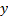 
described earlier)
depending on several different independent variables simultaneously. It can be
thought of as mathematically equivalent to univariate regression, except with
everything expressed using vectors rather than scalars.
4.2 There are several ways in which we can
generalise linear regression, including:
(a)
Multiple regression, in which the dependent variables depend on
several different independent variables simultaneously;
(b)
Heteroscedasticity, in which we assume that the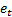 
have
different (known) standard deviations. We then adjust the weightings assigned
to each term in the sum, giving greater weight to the terms in which we have
greater confidence;
(c)
Autoregression, in which the dependent data series depends not
just on other independent data sets, but also on prior values of itself;
(d)
Autoregressive heteroscedasticity, in which the standard
deviations of the 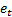vary
in some sort of autoregressive manner;
(e)
Generalised linear least squares regression, in which we assume
that the dependent variables are linear combinations of (linear) functions of
the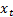 
.
Least squares regression is merely a special case of this, consisting of a
linear combination of two functions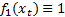 
and
;
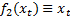(f)
Non-normal random terms, where we no longer assume that the
random terms are distributed as normal random variables. This is sometimes
called robust regression. This may involve distributions where the
maximum likelihood estimators minimise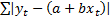 
in
which case the formulae for the estimators then involve medians rather than
means. We can in principle estimate the form of the dependency by the process
of box counting, which has close parallels with the mathematical concept
of entropy, see e.g. Press et
al. (2007) or Abarbanel et
al. (1993).
4.3 In all of the above refinements, if we know
the form of the error terms and heteroscedasticity then we can always transform
the relationship back to a generalised linear regression framework by
transforming the dependent variable to be linear in the independent variables.
The noise element might in such circumstances need to be handled using copulas
and the like.
4.4 It is thus rather important to realise that
only certain sorts of time series can be handled successfully within a linear
framework however complicated are the adjustments that we might apply as above.
All such linear models are ultimately characterised by a spectrum (or to be
more a precise z-transform) that in general involves merely rational
polynomials. Thus the output of all such systems is still characterised by
noise superimposed on combinations of exponential decay, exponential growth,
and regular sinusoidal behaviour.
We can
in principle identify the dynamics of such systems by identifying the
eigenvalues and eigenvectors of the corresponding matrix equations. If noise
does not overwhelm the system dynamics we should expect the
spectrum/z-transform to have a small number of distinctive peaks corresponding
to relevant zeros or poles applicable to the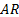 
or 
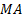elements.
We can postulate that these correspond to the underlying dynamics of the time
series.
4.5 Noise will result in the spreading out of the
power spectrum around these peaks. The noise can be ‘removed’ by replacing the
observed power spectrum with one that has sharp peaks, albeit not with perfect
accuracy (since we won’t know exactly where the sharp peak should be
positioned). For these sorts of time series problems, the degree of external
noise present is in some sense linked to the degree of spreading of the power
spectrum around its peaks.
4.6 However, the converse is not true. Merely
because the power spectrum is broad (and without sharp peaks) does not mean
that its broadband component is all due to external noise. Irregular behaviour
can still appear in a perfectly deterministic framework, if the framework is chaotic.
NAVIGATION LINKS
Contents | Prev | Next