Quantitative Return Forecasting
1. Introduction
[this page | pdf | references | back links]
Return to Abstract and
Contents
Next page
1.1 Many different techniques exist for trying to
predict or forecast the future movements of investment markets.
These range from purely judgemental to purely quantitative approaches and from
ones that concentrate on individual stocks to ones that are applied to sectors
or entire markets. In this set of pages on the Nematrian website we cover some
of the more quantitative tools that have been devised for this purpose. Many
very clever people have spent a lot of time devising quantitative ways of
forecasting future investment returns, so in these pages cover only some of the
many tools and techniques that might be used in practice.
1.2 Quantitative return forecasting can be
thought of as a special type of time series analysis. Hence many of the time
series analysis tools that are used in other contexts may also be applied to
quantitative investment analysis. Time series analysis can in turn be split
into two main types, both of which are typically analysed in a mathematical
context using regression techniques. These are:
(a) Analysis of the interdependence of two or
more variables measured at the same time, e.g. whether high inflation is
associated with high asset returns. The assumption here is that there is some
other exogenous way in which we can form an opinion on, say, how inflation will
move in the future, and we then use this together exogenous view, together with
an understanding of the interdependency of inflation and the asset return we
want to forecast or predict to work out the most appropriate investment stance
to adopt. The tools used are conceptually similar to those used for risk
measurement, except that with risk measurement we are typically seeking to
understand the spread of the distribution rather than its mean drift.
(b) Analysis of the interdependence of one or
more variables measured at different times, usually with some intuitive
justification proposed for the supposed interdependence being claimed from the
analysis. Such links (if they can be found and if they persist) can be used
directly to identify profitable investment strategies (as long as the excess
returns available from their use are not swamped by transactions costs).
1.3 A simple example of a problem of the type
described in 1.2(a) might involve postulating that there was some a linear
relationship involving two time series,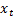 
and
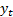(for
,
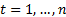where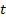 
is a suitable time index)
of the form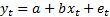 
where
the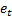 
are
random errors each with mean zero, an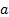d 
and
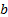are
unknown constants. The same relationship can be written in vector form as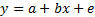 
where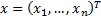 
is
a vector of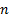 
elements corresponding to
each element of the time series etc. In such a problem the 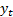are
called the dependent variables and the 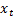the
independent variables, as in the postulated relationship the 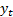depend
on the 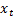not
vice-versa.
Such a
problem is most commonly solved by use of regression techniques, as explained
in many statistics textbooks. If the 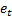are
independent identically distributed normal random variables with the same
variance (and same zero mean) then the maximum likelihood estimators of 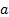and 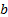are are
the values that minimise the sum of the squared forecast error, i.e.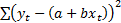 
.
These are also known as their least squares estimators. More generally,
we might adopt other ways of estimating these variables including minimising,
say, the mean absolute deviation, which involves minimising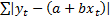 
.
1.4 To convert this simple example into one of
the sort described in 1.2(b) we might incorporate a one-period time lag in the
above relationship, i.e. we would assume that stocks, markets and/or factors
driving them exhibit autoregression.
1.5 Typically, the mathematical framework
involved can most easily be explained using vectors, see below. Mathematically
we assume that there is some equation governing the behaviour of the system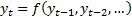 
.
The 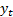might
now in general be vector quantities rather than scalar quantities, some of
whose elements might be unobserved state variables. However, the
simplest examples have a single (observed) series in which later terms depend
on former ones.
1.6 Traditional time series analysis generally
assumes, at that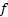 
exhibits time
stationarity (meaning it has the same functional form for each 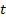). More
advanced variants might include regime shifts or the like, in which the model
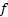of the world as characterised by can vary in some well
defined manner.
1.7 We shall see later that time stationary
models can only describe a relatively small number of possible market dynamics
(in effect just regular cyclicality and purely exponential growth or
decay). This is probably why traditional linear time stationary regression
techniques seem to be rather less effective than one might hope at directly
identifying profitable investment strategies.
1.8 Investment markets do show cyclical
behaviour, but the frequencies of the cycles are often far from regular. It is
easy to postulate variables that ought to influence markets, but much more
difficult to identify ones that seem to do so consistently whilst at the same
time offering significant predictive power. Relationships that work well over
some time periods often seem to work less well over others.
1.9 Perhaps this is not too surprising. If
successful forecasting techniques were easy to find then presumably this would
already be well known and market prices would have already reacted, reducing or
eliminating the potential of such forecasting techniques to add value in the
future. In this field, as in other aspects of active investment management, it
is necessary to stay one step ahead of others!
NAVIGATION LINKS
Contents | Prev | Next