The negative binomial distribution
[this page | pdf | back links]
The negative binomial distribution describes the probability
of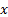 
successes in a
sequence of independent experiments each with likelihood of success of 
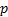that
arise before there are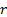 
failures. In this
interpretation 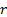is a positive
integer, but the distributional definition can also be extended to real values
of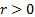 
. Note: different
texts adopt slightly different definitions, e.g. with support starting at 
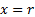not
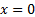and/or with 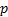denoting
probability of failure rather than probability of success.
|
Distribution name
|
Negative
binomial distribution
|
|
Common notation
|
|
|
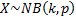
Parameters
|
=
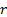number of failures ()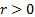
=
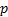probability of success in each experiment ( )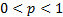
|
|
Support
|
|
|
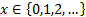
Probability mass
function
|
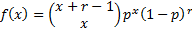
If 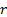is non-integral
then is:
|
|
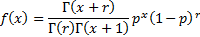
Cumulative distribution
function
|
|
|
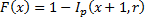
Mean
|
|
|
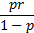
Variance
|
|
|
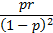
Skewness
|
|
|
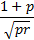
(Excess) kurtosis
|
|
|
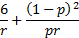
Characteristic function
|
|
|
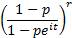
Other comments
|
The geometric distribution is the same as the
negative binomial distribution with parameter  .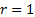
Its pdf and cdf are therefore:
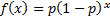
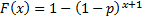
For the special case where 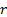is
an integer the negative binomial distribution is also called the Pascal
distribution. The Poisson
distribution is also a limiting case of the negative binomial:
|
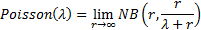
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “negative
binomial”. For details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next