The logarithmic distribution
[this page | pdf | back links]
The logarithmic distribution arises from following power
series expansion:
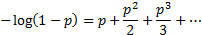
This means that the function 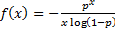 ,
, 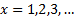 can
naturally be interpreted as a probability mass function since
can
naturally be interpreted as a probability mass function since 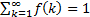 .
.
|
Distribution name
|
Logarithmic
distribution
|
|
Common notation
|
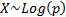
|
|
Parameters
|
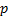 =
shape parameter ( =
shape parameter (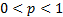 ) )
|
|
Domain
|
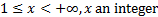
|
|
Probability mass
function
|
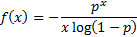
|
|
Cumulative distribution
function
|
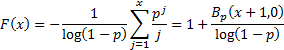
|
|
Mean
|
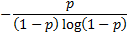
|
|
Variance
|
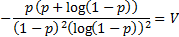
|
|
Skewness
|
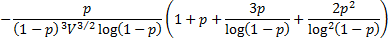
|
|
(Excess) kurtosis
|
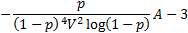
where
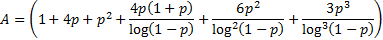
|
|
Characteristic function
|
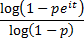
|
|
Other comments
|
The logarithmic distribution has a mode of 1. If 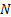 is
a random variable with Poission distribution and is
a random variable with Poission distribution and 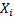 , , 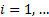 is
an infinite sequence of iid random variables each distributed is
an infinite sequence of iid random variables each distributed 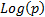 then then 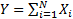 has a negative
binomial distribution showing that the negative binomial distribution is an
example of a compound Poisson distribution has a negative
binomial distribution showing that the negative binomial distribution is an
example of a compound Poisson distribution
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “logarithmic”.
For details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next