The hypergeometric distribution
[this page | pdf | back links]
The hypergeometric distribution describes the probability of
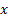 successes in
successes in 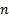 draws
from a finite population size
draws
from a finite population size 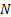 containing
containing 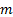 successes
without replacement. This contrasts with the binomial
distribution which describes the probability of
successes
without replacement. This contrasts with the binomial
distribution which describes the probability of 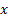 successes
in
successes
in 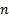 draws with
replacement
draws with
replacement
|
Distribution name
|
Hypergeometric
distribution
|
|
Common notation
|
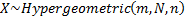
|
|
Parameters
|
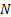 =
population size, integral ( =
population size, integral (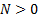 ) )
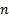 =
sample size, integral ( =
sample size, integral (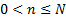 ) )
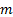 =
number of tagged items, integral ( =
number of tagged items, integral (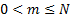 ) )
|
|
Domain
|
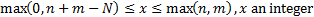
|
|
Probability mass
function
|
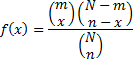
|
|
Cumulative distribution
function
|
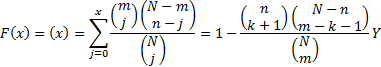
where
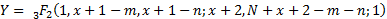
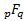 is the
generalised hypergeometric function, i.e. is the
generalised hypergeometric function, i.e.
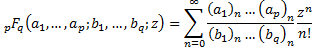
and 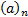 involves the
rising factorial or Pochhammer notation, i.e. involves the
rising factorial or Pochhammer notation, i.e. 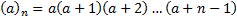 and and 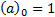
|
|
Mean
|
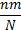
|
|
Variance
|
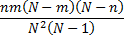
|
|
Skewness
|
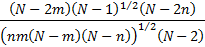
|
|
(Excess) kurtosis
|
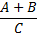
where
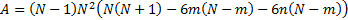
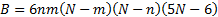
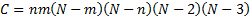
|
|
Characteristic function
|
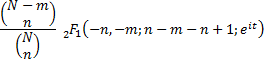
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “hypergeometric”.
For details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next