Interpolation and Extrapolation: Introduction

[this page | pdf | references | back links]

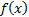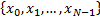Suppose we know the value that a function  takes at a set of points  say, where we have ordered the 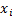 so that 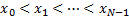. However we do not have an analytic expression for 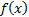 that allows us to calculate it at an arbitrary point. Often the 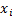’s are equally spaced, but not necessarily. How might we best estimate 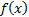 for arbitrary 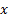 by in some sense drawing a smooth curve through and potentially beyond the 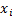? If 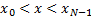, i.e. within the range spanned by the 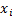 then this problem is called interpolation, otherwise it is called extrapolation.

To do this we need to model 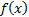, between or beyond the known points, by some plausible functional form. It is relatively easy to find pathological functions that invalidate any given interpolation scheme, so there is no single ‘right’ answer to this problem. Approaches that are often used in practice involve modelling 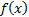 using polynomials or rational functions (i.e. quotients of polynomials). Trigonometric functions, i.e. sines and cosines, can also be used, giving rise to so-called Fourier methods.

The approach used can be ‘global’, in the sense that we fit to all points simultaneously (giving each in some sense ‘equal’ weight in the computation). More commonly, the approach adopted is ‘local’, in the sense that we give greater weight in the curve fitting to points ‘close’ to the value of 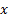 in which we are interested.

A simple example of a ‘local’ interpolation approach would be linear interpolation, implemented in the Nematrian website via the function MnLinearInterpolation. This involves finding the two points straddling the value of 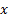 in which we are interested, say 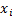 and 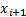 and identifying as the interpolated value the 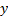 for which  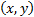lies along the straight line joining 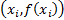 and 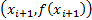. 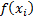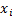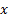In such an approach we give no weight at all to any of the  other than the two corresponding to the two  straddling the value of  in question. 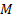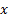More generally, we might use an approach that incorporates only the  nearest neighbours to the value of  in question. The number 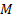 of points used, minus 1, is called the order of the interpolation scheme, so linear interpolation is a first order scheme. Increasing the order does not necessarily increase accuracy, especially with polynomial interpolation. Higher-order polynomials can often oscillate wildly between the tabulated points.

Simple nearest-neighbour arrangements in which we give no weight to any points beyond th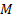e  nearest ones have a potentially significant weakness. The first and higher order derivatives of the resulting answers are discontinuous wherever the set of points deemed ‘local’ changes. To overcome this problem, practitioners often use spline functions, in which non-locality is introduced in a way that guarantees global smoothness in the interpolated function up to some given order of derivative.

Interpolation can be done in more than one dimension. Often this is accomplished by a sequence of one-dimensional interpolations, but there are other techniques applicable to scattered data, see e.g. Press et al. (2007).