Blending Independent Components and
Principal Components Analysis
2.5 Projection pursuit
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next page
2.5 Projection
pursuit
Suppose we focus further on the property of non-normality,
which we might measure via the (excess) kurtosis of a distribution. Kurtosis
has two properties relevant to ICA:
(a) All linear combinations
of independent distributions have a smaller kurtosis than the largest kurtosis
of any of the individual distributions (a result that can be derived using the
Cauchy-Schwarz inequality).
(b) Kurtosis is invariant
to scalar multiplication, i.e. if the kurtosis of distribution 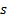 is
is 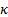 then the
kurtosis of the distribution defined by
then the
kurtosis of the distribution defined by 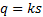 where
where 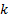 is constant is
also
is constant is
also 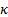 .
.
Suppose we also want to identify the input signals (up to a
scalar multiple) one at a time, starting with the one with the highest
kurtosis. This can be done via projection pursuit.
Given (a) and (b) we can expect the kurtosis of 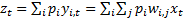 to be
maximised when this results in
to be
maximised when this results in 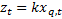 for the
for the 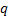 corresponding
to the signal
corresponding
to the signal 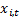 which has the largest
kurtosis, where
which has the largest
kurtosis, where 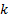 is arbitrary.
Without loss of generality, we can reorder the input signals so that this one
is deemed the first one, and thus we expect the kurtosis of
is arbitrary.
Without loss of generality, we can reorder the input signals so that this one
is deemed the first one, and thus we expect the kurtosis of 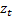 to be
maximised with respect to
to be
maximised with respect to 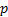 when
when 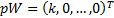 and
and 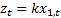 . Although we
do not at this stage know the full form of
. Although we
do not at this stage know the full form of 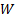 we have still
managed to extract out one signal (namely the one with the largest kurtosis)
and found out something about
we have still
managed to extract out one signal (namely the one with the largest kurtosis)
and found out something about 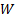 .
.
In principle, the appropriate value of 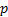 can
be found using brute force exhaustive search, but in practice more efficient
gradient based approaches would be used instead, see Section
2.8.
can
be found using brute force exhaustive search, but in practice more efficient
gradient based approaches would be used instead, see Section
2.8.
We can then remove the recovered source signal from the set
of signal mixtures and repeat the above procedure to recover the next source
signal from the ‘reduced’ set of signal mixtures. Repeating this iteratively,
we should extract all available source signals (assuming that they are all
lepto-kurtotic, i.e. all have kurtosis larger than any residual noise, which we
might assume is merely normally distributed). The removal of each recovered
source signal involves a projection of an 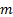 -dimensional
space onto one with
-dimensional
space onto one with 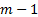 dimensions and
can be carried out using Gram-Schmidt orthogonalisation.
dimensions and
can be carried out using Gram-Schmidt orthogonalisation.
With any blind source separation method, a fundamental issue
that has no simple answer is when to truncate such a search. If the mixing
processes were noise free then the truncation should stop having extracted
exactly the right number of signals (as long as there are at least as many
distinct output signals as there are input signals). However, outputs are
rarely noise free. In practice, therefore, we might truncate the signal search
once the signals we seem to be extracting via it appear to be largely artefacts
of noise in the signals or mixing process, rather than suggestive of additional
true underlying source signals.
We see similarities with random matrix theory,
an approach used to truncate the output of a principal components analysis to
merely those principal components that are probably not just artefacts of noise
in the input data.
NAVIGATION LINKS
Contents | Prev | Next