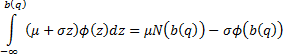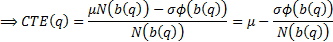Identifying a formula for the (lower)
conditional tail expectation (CTE) of a normal distribution that does not
explicitly include integral signs but instead refers to the unit normal density
function and the unit normal cumulative distribution function
[this page | pdf | back links]
The (lower) conditional tail expectation (CTE) of a random
variable for a given cut-off, 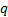 , is
defined as the expected value of the random given that it is below the relevant
cut-off. It is thus very closely aligned with the Tail Value-at-Risk
(TVaR) of the distribution, since the TVaR is the CTE for a specific cut-off.
For a normal
distribution the CTE is thus:
, is
defined as the expected value of the random given that it is below the relevant
cut-off. It is thus very closely aligned with the Tail Value-at-Risk
(TVaR) of the distribution, since the TVaR is the CTE for a specific cut-off.
For a normal
distribution the CTE is thus:
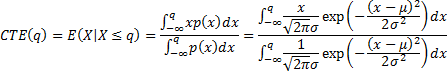
The unit normal distribution function, 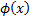 , and
the unit Normal cumulative distribution function,
, and
the unit Normal cumulative distribution function, 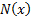 , are
defined as follows:
, are
defined as follows:
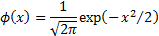
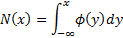
Substituting 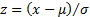 in the
above formula for the CTE we obtain, where
in the
above formula for the CTE we obtain, where 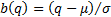 ):
):
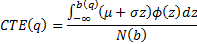
We can re-express this in a form that relies only on 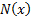 and
and 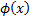 by
noting the following:
by
noting the following:
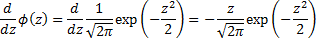
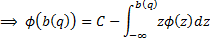
where 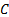 is
constant and furthermore as
is
constant and furthermore as 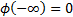 and
and 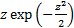 decays
sufficiently fast to zero as
decays
sufficiently fast to zero as 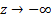 we have
we have
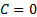 . Hence:
. Hence: