Enterprise Risk Management Formula Book
10. Portfolio optimisation
[this page | pdf | back links]
10.1 Mean-variance
portfolio optimisation
If there are 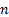 asset
categories then a (one period) mean-variance efficient portfolio,
asset
categories then a (one period) mean-variance efficient portfolio, 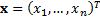 where
where 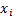 is the
amount (or weight) invested in the
is the
amount (or weight) invested in the 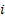 ’th asset,
given a benchmark,
’th asset,
given a benchmark, 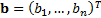 , assumed
future (one period) mean returns on each asset,
, assumed
future (one period) mean returns on each asset, 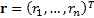 , and an
assumed covariance matrix between the (one period) returns on different assets,
, and an
assumed covariance matrix between the (one period) returns on different assets,
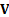 , is a
portfolio that maximises the utility function,
, is a
portfolio that maximises the utility function, 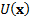 for some
risk aversion parameter,
for some
risk aversion parameter, 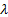 , subject
to relevant constraints on the
, subject
to relevant constraints on the 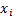 , where:
, where:
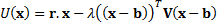
The constraints that are applied are usually linear, i.e. of
the form 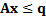 which if
which if 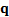 is an
is an 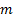 dimensional
vector is understood as meaning that there are
dimensional
vector is understood as meaning that there are 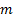 constraints
each of the form
constraints
each of the form 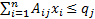 . In such a
formulation, equality constraints, including that the amounts invested add up
to the total portfolio value (or the weights add to unity), can be written as
two inequality constraints, e.g.
. In such a
formulation, equality constraints, including that the amounts invested add up
to the total portfolio value (or the weights add to unity), can be written as
two inequality constraints, e.g. 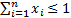 and
and 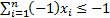 combined.
combined.
The implied alphas with a mean-variance risk-return model
given a portfolio 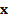 and
benchmark
and
benchmark 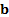 are the
mean returns that need to be assumed for the different asset categories for
are the
mean returns that need to be assumed for the different asset categories for 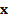 to be
mean-variance optimal for some value of
to be
mean-variance optimal for some value of 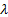 . They can
only meaningfully be determined for assets whose weights in the portfolio are
not constrained (other than by the constraint that weights add to unity). They
are then
. They can
only meaningfully be determined for assets whose weights in the portfolio are
not constrained (other than by the constraint that weights add to unity). They
are then 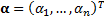 where
where 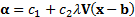 where
where 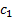 and
and 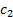 are
arbitrary scalar constants.
are
arbitrary scalar constants.
10.2 Capital Asset Pricing Model (CAPM)
The security market line is:
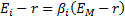
where 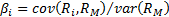
The capital market line (for efficient portfolios) is:
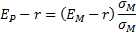
NAVIGATION LINKS
Contents | Prev | Next