Coherent Risk Measures
[this page | pdf | references | back links]
A risk measure, 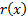 is
defined by Artzner et al. (1999) to be coherent if it satisfies the following 4
axioms:
is
defined by Artzner et al. (1999) to be coherent if it satisfies the following 4
axioms:
(a) Subadditivity:
for any pair of loss variables, 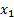 and
and
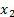
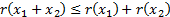
(b) Monotonicity:
if, for all states of the world, 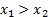 then
then
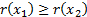
(c) Homogeneity:
for any constant 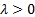 and random loss variable
and random loss variable 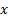
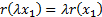
(d) Translational
invariance: for any constant 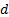 and random loss variable
x
and random loss variable
x
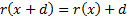
Artzner et
al. (1999) also showed that a risk measure is coherent if and only if there
is a family,  , of probability measures,
, of probability measures,
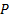 ,
such that:
,
such that:
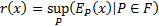
Sometimes the easiest way of proving that a risk measure is
coherent is to prove each of the four axioms are satisfied, at other times it
is easiest to show that it may be expressed in this supremum form.
For example TVaR can be shown to
be coherent by defining a set of probability measures that place equal
probability on  realisations where
realisations where  is the
smallest integer such that
is the
smallest integer such that 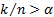 .
TVaR is then the maximum expected value of losses over this family of
distributions.
.
TVaR is then the maximum expected value of losses over this family of
distributions.
In contrast, VaR is coherent only for a
limited class of distributions, including multi-variate Normal (i.e. Gaussian)
distributions (for proof see here)
and more generally for elliptical
distributions.