Testing Investment Manager Skill
[this page | pdf | back links]
Because investment management involves seeking an
appropriate balance between risk and reward, assessment of manager skill
generally focuses on measures that takes due account of both of these factors.
The most common statistic used, at least for managers who
have an outperformance target relative to a benchmark is thus the Information
Ratio, which is calculated as:
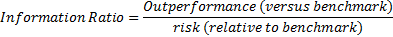
Here, outperformance is relative return (possibly annualised,
and possibly also converted into geometric or
logarithmic form). Risk is measured by reference to standard deviation of
relative return.
The corresponding statistic, if the benchmark is cash (or an
absolute performance objective) is the Sharpe ratio, see Risk Measurement
Glossary.
Effectively, the Information Ratio is measuring the
outperformance per unit of risk taken (i.e. ‘bangs per buck’). If all relative
positions were doubled in size (and assuming that the investor only holds a
small proportion of the total of such exposures, so such a doubling does not in
practice increase the investor’s liquidity risk), then outperformance and risk,
as measured above, should both double and hence the Information Ratio should
remain unaltered. So the Information Ratio measures the skill at selecting and
implementing investment ideas as it is invariant to the amount of capital put
to work with these ideas.
The use of standard deviations to measure risk implicitly
assumes that returns are not fat-tailed or that the investor is indifferent to
fat-tailed behaviour to the extent that it does exist. Either the Information
Ratio or the Sharpe ratio can be refined to use other measures of risk deemed
more appropriate by the investor, e.g. downside risk (see Sortino ratio in Risk Measurement
Glossary) or measures that give greater importance to fat-tailed behaviour,
akin to those used for independent
components analysis.
If returns are log-normally distributed then the information
ratio (if outperformance and risk are both expressed logarithmically) is the
same as the t-statistic that would be used to test for the mean of the
distribution being significantly different from zero.
If we further assume that investment manager ‘skill’ is
relatively rare (an assumption that seems to be approximately true for many
asset types) then we should expect the spread of Information Ratios that a
selection of active managers (e.g. a peer group of funds all investing in the
same asset class) to be distributed in the same way as the corresponding t-statistic
would be distributed under the null hypothesis that the mean (relative) return
is zero. Such a methodology can be used to estimate the information ratio level
needed to be, say, upper quartile in such a peer group. For large 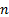 , where
, where 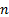 is the
number of funds in the peer group, the distribution tends to a normal
distribution independent of
is the
number of funds in the peer group, the distribution tends to a normal
distribution independent of 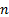 and hence independent of
the peer group in question.
and hence independent of
the peer group in question.
If we make further assumptions about the typical spread of
risk that different managers in a given peer group might exhibit, we can derive
approximations for the level of risk that a manager needs to take to achieve an
upper quartile performance given a specific level of skill. For many peer
groups an approximately median level of risk coupled with an upper quartile
information ratio appears to equate to approximately an upper quartile
performance.