Solar-powered space flight
4. Taking into account atmospheric drag
[this page | pdf | references | back links]
Copyright (c) Malcolm
Kemp 2009
Return to Abstract
and Contents
Next page
4. Taking into
account atmospheric drag
4.1 The most
obvious way of overcoming air resistance early on in the flight is to use a
chemical rocket to lift the vehicle above the atmosphere before then deploying
the solar collector and commencing solar-powered flight.
4.2 It is worth
exploring how far up is ‘above’ in this context. We might model the drag force
per unit cross-sectional area perpendicular to the velocity vector as 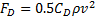 .
. 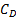 is likely to be near
its maximum value of 2.6, given the shape of the mirror layout, which means
that
is likely to be near
its maximum value of 2.6, given the shape of the mirror layout, which means
that 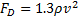 . If we assume that
the collector has a mass per unit surface area perpendicular to the velocity
vector of, say, 5 g m-2 (see later), and we ignore any other
contributor to the mass of the vehicle, then Table 5 shows the maximum speed
(at different altitudes) at which the vehicle can travel if we want the drag
deceleration to be no more than, say, 1 ms-2 (i.e. 0.1g) We
have here used atmospheric densities derived from Kaye &
Laby(1986) (above 30 km the edition quoted in the References does not
directly quote densities, so these have been estimated by applying the Gas Law
to data that is quoted there, high precision not being particularly relevant
for our purposes here):
. If we assume that
the collector has a mass per unit surface area perpendicular to the velocity
vector of, say, 5 g m-2 (see later), and we ignore any other
contributor to the mass of the vehicle, then Table 5 shows the maximum speed
(at different altitudes) at which the vehicle can travel if we want the drag
deceleration to be no more than, say, 1 ms-2 (i.e. 0.1g) We
have here used atmospheric densities derived from Kaye &
Laby(1986) (above 30 km the edition quoted in the References does not
directly quote densities, so these have been estimated by applying the Gas Law
to data that is quoted there, high precision not being particularly relevant
for our purposes here):
Table 5. Impact of
atmospheric drag at different altitudes
|
Altitude above
earth’s surface (km)
|
Approximate
atmospheric density (kg m-3)
|
Approximate
velocity (ms-1) below which drag would be below 0.1g for
arrangements with mass 5 g m-2
|
|
0
|
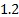
|
0.06
|
|
50
|
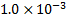
|
1.9
|
|
100
|
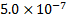
|
88
|
|
150
|
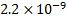
|
1,334
|
|
200
|
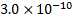
|
3,587
|
|
300
|
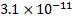
|
11,127
|
|
500
|
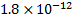
|
46,512
|
|
800
|
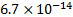
|
239,840
|
4.3 At an
altitude of, say, 500km (or above), the atmospheric drag that the vehicle would
experience is likely to be negligible in relation to any of the accelerations
envisaged by trajectories described in the previous section, even if the
vehicle was travelling at close to orbital velocity. At this altitude the pull
of gravity is also somewhat less than at the surface of the earth, as is the
orbital velocity. Lower values of 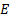 per unit lifted mass
will then suffice to reach orbit having first reached this altitude with
chemical rocketry, particularly if we also use the initial chemical rocket
stage to impart horizontal velocity, see Figure 6. This might bring the
required mirror mass closer to what might be within current technological
capability.
per unit lifted mass
will then suffice to reach orbit having first reached this altitude with
chemical rocketry, particularly if we also use the initial chemical rocket
stage to impart horizontal velocity, see Figure 6. This might bring the
required mirror mass closer to what might be within current technological
capability.
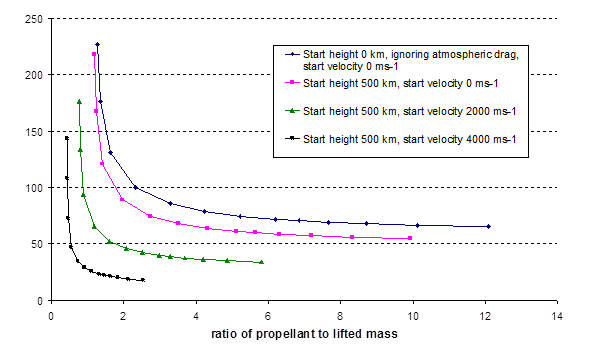
Figure 6. Values of 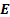 (for different
propellant to lifted mass ratios), assuming vehicle travels horizontally with
propellant ejected at optimal speeds (subject to an upper limit of 10,000 ms-1)
and angles, if chemical rocketry is used to launch the vehicle above the
earth’s atmosphere and to impart initial horizontal velocity
(for different
propellant to lifted mass ratios), assuming vehicle travels horizontally with
propellant ejected at optimal speeds (subject to an upper limit of 10,000 ms-1)
and angles, if chemical rocketry is used to launch the vehicle above the
earth’s atmosphere and to impart initial horizontal velocity
4.4 Of course,
the faster the vehicle reaches before it starts using solar-powered propulsion
the greater would be the chemical propellant that it would need to reach this
speed. But it is interesting to note that a liquid hydrogen/liquid oxygen
chemical rocket as used by, say, the NASA Space Shuttle accelerating from 4,000
ms-1 to the orbital velocity at this height (circa 7,600 ms-1)
would itself require propellant of at least circa 1.2 times the lifted mass in
this stage (if the rocket had a specific impulse of 450 s). This multiple is
not dissimilar to that applicable to an equivalent solar-powered vehicle, if 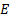 were
of the order of 25 kW/kg.
were
of the order of 25 kW/kg.
4.5 It might be
practical to start solar-powered propulsion at an altitude materially below 500
km (although most probably not from ground level) if the rate of ascent was
carefully optimised and if the vehicle only started to acquire appreciable
horizontal velocity after it had reached a suitable altitude. It might even be
possible for this lower starting altitude to be reached via methods other than
conventional rocketry, e.g. by use of air-breathing engines or ultra-high
altitude balloons. These possibilities are not explored further in this note.
NAVIGATION LINKS
Contents | Prev | Next