Derivative Pricing – Semi-Analytic
Lattice Integrator Approaches
2. Carrying out the required integrations
[this page | pdf | references | back links]
Return
to Abstract and Contents
Next
page
2.1 There are several possible choices for the
‘basis’ function elements of SALI, i.e. the 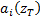 . If
we are focusing on a single factor model, then
. If
we are focusing on a single factor model, then 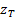 is a
scalar function rather than a vector function. Natural choices of basis
functions are then:
is a
scalar function rather than a vector function. Natural choices of basis
functions are then:
(a) Low-order
piece-wise smooth polynomials, such as cubic splines. Only a few node points
are usually necessary to obtain a pretty accurate representation of a smooth
function. Hu,
Kerkhof, McCloud and Wackertapp (2006) focus on this approach.
(b) Higher order
polynomial curve fits. There are many different ways of approximating
arbitrarily accurately a function over a given range by using a polynomial
series expansion, typically formulated using orthogonal polynomials, e.g.
Legendre polynomials.
(c) Curve fits using
other function series that can arbitrarily accurately approximate a function
over a given range, where the functions in question are more easily or more
accurately capable of being integrated against the probability density in
question or can more succinctly match the payoff function in question.
2.2 One reason why (c) may be better than (b) can
be seen by considering how SALI might be applied to the special case of
European-style vanilla call and put options in a Black-Scholes world (for which
there are already analytic formulae, see hedging parameters
applicable to vanilla and binary puts and calls in a Black-Scholes world). The
underlying process (for a non-dividend bearing underlying) in this case
involves:
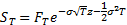
where 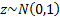 .
.
Thus the natural curve
fit to use in this instance is an exponential, since we then recover exactly
the Black-Scholes formulae, see e.g. Black-Scholes
derivation using stochastic calculus. This corresponds to polynomial curve
fitting of 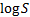 rather
than
rather
than 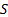 itself.
itself.
2.3 Various analytical results that can be used in
this context when the payoff function is approximated using basis elements that
are either polynomials or exponentials of polynomials (if the underlying
follows a Weiner process or some straightforward variants) are described in integration
of piece-wise polynomials against a Gaussian PDF.
NAVIGATION LINKS
Contents | Prev | Next