Quantitative Return Forecasting
7. Locally linear time series analysis
[this page | pdf | references | back links]
Return to Abstract and
Contents
Next page
7.1 One
possible reason why neural networks were originally found to be relatively poor
at financial problems is that the effective signal to noise ratio involved in
such problems may be much lower than for other types of problem where they have
proved more successful. In other words there is so much random behaviour that can’t
be explained by the inputs that they struggle to make much sense of it.
7.2 But
even if this is not the case, it seems to me that disillusionment with neural
networks was almost inevitable. Mathematically, our forecasting problem
involves attempting to predict the immediate future from some past history. For
this to be successful we must implicitly believe that the past does offer some
guide to the future. Otherwise the task is doomed to failure. If the whole
of the past is uniformly relevant to predicting the immediate future then, as
we have noted above, a suitable transformation of variables moves us back into
the realm of traditional linear time series, which we might in this context
call globally linear time series analysis. To get the sorts of broadband
characteristics that real time series return forecasting problems seem to
exhibit you must therefore be assuming that some parts of the past are a better
guide for forecasting the immediate future than other parts of the past.
7.3 This
perhaps explains growth in interest in models that include the possibility of
regime shifts, e.g. threshold autoregressive (TAR) models or refinements. These
assume that the world can be in one of two (or more) states, characterised by,
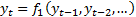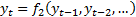say, 
,
, ... and that there is some hidden variable indicating which of these two (or
more) world states we are in at any given time. We then estimate for each
observed time period which state we were most likely to have been in at that point
in time, and we focus our estimation of the model applicable in these instances
to information pertaining to these times rather than to the generality of past
history.
7.4 More
generally, in some sense what we are trying to do is to:
(a)
Identify the relevance of a given element of the past to forecasting the
immediate future, which we might quantify in the form of some mathematical
measure of ‘distance’, where the ‘distance’ between a highly relevant element
of past and the present is deemed to be small, whilst for a less relevant
element the ‘distance’ is greater; and
(b) Carry out what is now
(up to a suitable transform) a locally-linear time series analysis (only
applicable to the current time), in which you give more weight to those
elements of the past that are ‘closer’, in the sense of (a), to present
circumstances, see e.g. Abarbanel et
al. (1993) or Weigend
& Gershenfeld (1993).
7.5 Such
an approach is locally linear in the sense that it involves a linear
time series analysis but only using data that is ‘local’ (i.e. deemed relevant
in a forecasting sense) to current circumstances. It is also implicitly how
non-quantitative investment managers think. One often hears them saying that
conditions are (or are not) similar to “the bear market of 1973-1994”, “the
Russian Debt Crisis”, “the Asian crisis” etc., the unwritten assumption being
that what happened then is (or is not) some reasonable guide to what might
happen now.
7.6 Such
an approach also:
(a)
Caters for any feature of investment markets that you think is truly
applicable in all circumstances, since this is the special case where we deem
the entire past to be ‘local’ to the present in terms of its relevance to
forecasting the future.
(b) Seems to encompass as
special cases any alternative threshold autogressive model, because these can
merely be thought of as special ways of partitioning up how such distances
might be characterised.
7.7 Such an approach thus provides a true
generalisation of traditional time series analysis into the chaotic domain.
7.8 This
approach also provides some clues as to why neural networks might run into
problems. In such a conceptual framework, the neural network training process
can be thought of as some (relatively complicated) way of estimating the
underlying model dynamics. A danger is that we start off with an initial
definition of the class of neural networks that is then sifted through for a
‘good fit’ that is hugely over-parameterised. The training process should
reduce this over-parameterisation, but by how much? If we fortuitously choose a
good set of possible neural network structures to sift through, or if our
training of the network is fortuitously good, then the neural network should
perform well, but what are the odds of this actually occurring?
7.9 Of
course, it can be argued that a locally linear time series analysis approach
also includes potential over-parameterisation in the sense that there is almost
unlimited flexibility in how you might define ‘distance’ between different
points in time. Indeed, perhaps the flexibility here is mathematically
equivalent to the flexibility of structure contained within the neural network
approach, since any neural network training approach can be reverse engineered
to establish how much weight is being given to different pasts for each
component of the training data. However, the flexibility inherent in choice of
‘distances’ is perhaps easier for humans to visualise and understand than other
more abstract ways of weighting past data.
7.10 Maybe
the neural networkers had it the wrong way round. Maybe the neural networks
within our brains are evolution’s way of approximating to the locally linear
framework referred to above. Or maybe consciousness, that elusive God-given
characteristic of humankind, will forever remain difficult to understand from a
purely mechanical or mathematical perspective.
NAVIGATION LINKS
Contents | Prev | Next