Different ways of calculating relative returns
[this page | pdf | back links]
Conventionally, a fund’s return relative to a benchmark
return is calculated as the arithmetic difference between the two (perhaps both
annualised, following some specified annualisation
convention), i.e. as 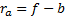 , where
, where 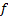 is
the fund return and
is
the fund return and 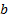 is the benchmark
return. This is known as an arithmetic relative return.
is the benchmark
return. This is known as an arithmetic relative return.
Returns compound through time, and hence log returns add
through time. It is therefore usually theoretically more appropriate to focus
on logarithmic relative returns, i.e.:
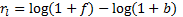
Here, 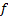 and
and 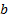 need
to be quoted as fractions, i.e. an arithmetic return of 10% is represented by
0.1, and it is conventional to use natural logarithms, so its corresponding log
return is
need
to be quoted as fractions, i.e. an arithmetic return of 10% is represented by
0.1, and it is conventional to use natural logarithms, so its corresponding log
return is 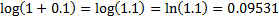 .
.
However, logarithms are not a universally well understood
concept amongst the readers of performance reports, who do not necessarily have
a mathematical or scientific background. A hybrid that is thus commonly used is
to quote geometric relative returns, defined as:
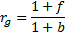
Again, 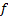 and
and 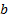 need
to be quoted as fractions.
need
to be quoted as fractions.
The Nematrian performance measurement functions generally
allow the user to choose between these different conventions, where relevant.
We may then define corresponding relative risk measures,
such as ex ante tracking error (which is inherently a relative risk measure)
and relative Value-at-Risk (i.e. relative VaR).