Derivative Pricing Theory: Optimising a
trinomial lattice to converge more rapidly than a binomial lattice
[this page | pdf | references | back links]
In a situation where 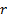 ,
, 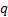 and
and
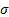 are constant
through time, a trinomial lattice framework that seems to provide effective
enhancements in convergence properties is as set out in Kemp (1997).
Suppose
are constant
through time, a trinomial lattice framework that seems to provide effective
enhancements in convergence properties is as set out in Kemp (1997).
Suppose 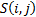 characterises the
lattice point in which we have had
characterises the
lattice point in which we have had 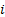 time steps from
outset and we are
time steps from
outset and we are 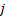 steps above the
lowest possible that is included in the trinomial tree. We propose a lattice
calculated as follows. Movement should be allowed from
steps above the
lowest possible that is included in the trinomial tree. We propose a lattice
calculated as follows. Movement should be allowed from 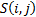 to
to 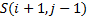 (i.e. up,
(i.e. up, 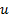 ),
),
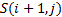 (sideways,
(sideways, 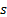 )
or
)
or 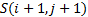 (down,
(down, 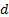 ),
with the nodes of the lattice defined by
),
with the nodes of the lattice defined by 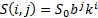 for some
for some 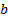 and
and
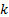 defined as below.
The backwards equation is then defined as follows:
defined as below.
The backwards equation is then defined as follows:
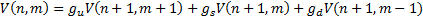
where: 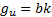 ,
, 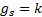 ,
, 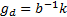 ,
, 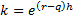 ,
, 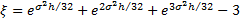 ,
, 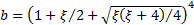 and additionally
and additionally 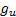 ,
, 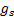 and
and 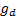 are chosen so that
the following three simultaneous equations are satisfied:
are chosen so that
the following three simultaneous equations are satisfied:
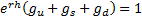
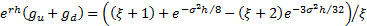
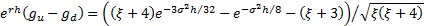
Such a lattice is
designed so that if we were to price a derivative paying 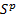 for each of
for each of 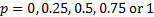 , then the lattice would
give exactly the right answer. For standard types of European and American
options this calibrated trinomial lattice can converge much more rapidly than
the equivalent binomial lattice. If
, then the lattice would
give exactly the right answer. For standard types of European and American
options this calibrated trinomial lattice can converge much more rapidly than
the equivalent binomial lattice. If 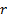 ,
, 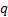 and
and
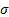 change through time
(in a deterministic way) then corresponding lattices (including risk-neutral
lattice migration probabilities) can be derived in an analogous fashion with
the same end goal, but the formulae involved will be time-varying and therefore
more complicated.
change through time
(in a deterministic way) then corresponding lattices (including risk-neutral
lattice migration probabilities) can be derived in an analogous fashion with
the same end goal, but the formulae involved will be time-varying and therefore
more complicated.
The complexity of the
above highlights an important practical aspect of derivative pricing. Whilst
the principles are in some sense conceptually relatively easy to grasp, the
mathematics can get complicated very quickly as soon as you start trying to
apply the concepts in practice, particularly if you want to do so in ways that
are relatively efficient to compute. It is not always clear how complex it
might be best to get in such a quest. For example:
(a) We might expect
to be able to improve convergence still further by using quadrinomial or even
more complicated lattices, but the effort involved in programming them becomes
progressively more complicated, and it becomes less easy to ensure that the
optimal lattice structure is recombining, so for fast numerical computation of
options using lattices, trinomial lattices are likely to be preferred over more
complex lattices in most circumstances.
(b) There are actually two
main sorts of errors arising with lattice pricing methods. The first sort of
error relates to propagation errors via the backwards equation, which can be
much reduced by using trinomial lattices rather than binomial ones. The second
sort of error involves the approximation of a continuous pay-off at maturity
with one involving discrete amounts at each maturity node. It can be reduced
by setting the pay-off at each maturity node equal to the average of maturity
pay-off for prices of the underlying closest to the node. This second sort of
error is not improved merely by use of a trinomial lattice. Typically better
still is to use semi-analytic lattice integrator approaches, see e.g. Hu, Kerkhof,
McCloud and Wackertapp (2007) or Semi-analytic
lattice integrator approaches, if the payoff function can be approximated
by piecewise polynomials and the risk-neutral probability distribution is
analytically tractable.
(c) Other ways exist
of improving convergence of binomial lattices not (directly) involving
trinomial lattices or the like. Because the pricing formulae can be rewritten
as expectations (under the risk neutral probability distribution) and because
expectations are merely specific instances of the mathematical process of
integration, lattices can be thought of as approximate ways of carrying out
integration. Various mathematical tools and techniques exist that can be
applied to this task, see e.g. Press et
al. (2007). Some of these tools appear to be as good as if not better
than using trinomial lattices (and even if they are not actually better they
may be rather simpler to understand and program reliably).
See also MnOptimisedTrinomialLatticeProbs.