ReverseQuadraticPortfolioOptimiser
[this page | pdf | back links]
Function Description
Returns a vector containing the ‘implied alphas’ for a given
set of active positions, i.e. the return assumptions that need to be held for a
portfolio to be optimal (ignoring constraints), given active positions,
standard deviations, a correlation matrix and a trade-off factor (i.e. risk
aversion factor) that corresponds to the investor’s chosen trade-off between
return and risk. It is assumed that the investor has a quadratic utility
function of the following form, where 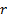 is a
vector of returns,
is a
vector of returns, 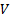 is a covariance
matrix and
is a covariance
matrix and 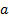 is a
vector of active weights (i.e.
is a
vector of active weights (i.e. 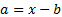 , where
, where 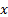 is
a vector of portfolio weights with
is
a vector of portfolio weights with 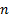 elements
and
elements
and 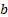 is the
corresponding vector of benchmark weights):
is the
corresponding vector of benchmark weights):
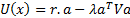
Please bear in mind that if a given set of returns, 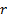 ,
is optimal in this context then so is the set of returns defined by
,
is optimal in this context then so is the set of returns defined by 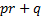 for
any constant (scalar, i.e. asset class independent) values of
for
any constant (scalar, i.e. asset class independent) values of 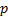 and
and
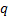 . This
function adopts the convention that
. This
function adopts the convention that 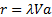 or
equivalently
or
equivalently 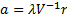 , i.e.
that
, i.e.
that 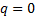 and that
and that 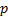 scales
in line with the risk-return trade-off factor, i.e.
scales
in line with the risk-return trade-off factor, i.e. 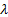 .
.
Please also bear in mind that if the active position within
a live portfolio is at the limit of a constraint (e.g. for a long-only
portfolio the portfolio weight is zero, i.e. constrained by the long-only
constraint) then it is not possible to calculate accurately the implied alpha
for that position, since we do not then know (merely from the portfolio
weights) how positive or negative is the view that the manager is assigning to
that position.
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other Portfolio optimisation functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement