/

CornishFisher4

[this page | pdf | back links]

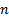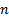Returns an array of  elements containing the quantiles predicted by the 4th moment Cornish-Fisher asymptotic expansion for a given input array of probability levels (with  elements), for a given mean, standard deviation, skew and (excess) kurtosis.

 

The Cornish-Fisher asymptotic expansion is a methodology for predicting the shape of a (univariate) distributional form merely from the moments of the distribution. The 4th moment variant uses the mean, standard deviation, skew and (excess) kurtosis of the distribution.

 

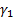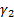For standardised returns (zero mean, unit standard deviation), the 4th moment variant involves estimating the shape of the quantile-quantile plot of the actual versus (standard) Normal distribution using the following cubic equation, where  is the skew and  is the (excess) kurtosis of the distribution:

 

 

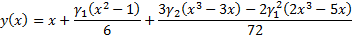
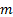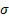In the more generalised case where the mean, , is not necessarily zero and the standard deviation,  is not necessarily unity the 4th moment variant involves estimating the shape of the quantile-quantile plot as follows:

 

 

---

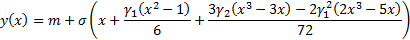
NAVIGATION LINKS
Contents | Prev | Next

---

-          Interactively run function

-          Interactive instructions

-          Example calculation

-          Output type / Parameter details

-          Illustrative spreadsheet

-          Other Risk management functions

-          Computation units used

Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement

---