CholeskyDecomposition
[this page | pdf | back links]
Function Description
Returns the Cholesky decomposition, L, of a square
matrix, A.
If A has real entries, is symmetric and is positive
definite then this decomposition involves expressing it in the form 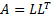 where L is a
lower triangular matrix with strictly positive diagonal entries and
where L is a
lower triangular matrix with strictly positive diagonal entries and 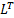 is its transpose. The
entries of L are:
is its transpose. The
entries of L are:
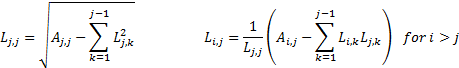
Cholesky decomposition has two main uses:
(a) Suppose we draw
vectors of independent normal random variables, 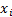 then
then 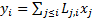 are vectors drawn from
a multivariate normal distribution with covariance matrix
are vectors drawn from
a multivariate normal distribution with covariance matrix 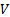 .
.
(b) A covariance matrix is
non-negative definite. Perhaps the easiest way to test if a symmetric matrix is
non-negative definite is to see if a Cholesky decomposition can be applied to
it.
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other Statistical functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement