CGamma
[this page | pdf | references | back links]
Function Description
Returns 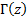 ,
the value of the gamma function evaluated for a complex number,
,
the value of the gamma function evaluated for a complex number, 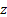 . The gamma
function,
. The gamma
function, 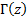 is
defined as:
is
defined as:
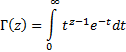
It can thought of as an extension of the factorial function,
but offset by one, since it satisfies the following recurrence relationship: 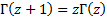 .
.
The Nematrian website calculates this value using a Lanczos approximation
and a reflection formula, see MnGamma.
For details of how to pass complex numbers to and from the
Nematrian website and on principal values of complex-valued functions please
see Complex Numbers
Introduction.
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other Complex numbers functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement