Kendal’s tau
[this page | pdf | back links]
Kendal’s tau is a measure of rank correlation and measures
the similarity of orderings of data when ranked by each of the quantities.
If 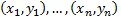 are
a set of joint observations from two random variables
are
a set of joint observations from two random variables 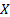 and
and 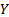 then pairs
then pairs 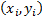 and
and
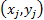
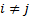 are said to be
‘concordant’ if both
are said to be
‘concordant’ if both 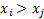 and
and
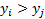 (or
if both
(or
if both 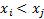 and
and
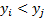 ).
They are said to be ‘discordant’ if
).
They are said to be ‘discordant’ if 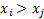 and
and
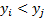 or
if
or
if 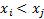 and
and
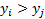 (and
neither concordant or discordant if if
(and
neither concordant or discordant if if 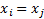 or
or
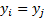 ,
which will not happen if all the
,
which will not happen if all the 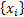 and
all the
and
all the 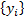 are
unique).
are
unique).
Kendall’s 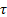 coefficient is then:
coefficient is then:
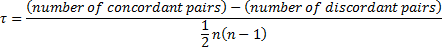
As there are 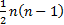 pairs
in total, the coefficient is in the range
pairs
in total, the coefficient is in the range 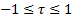 .
.
[N.B. There are various different ways of handling ties]
It is a non-parametric statistic and focuses just on
ordering, i.e. on behaviour of the copula, and not the individual marginal
distributions. This accords with how copulas are
specified. For certain copula families, the parameter that selects between
different members of the family has a one-to-one relationship with Kendal’s tau
(e.g. the Clayton
copula). A natural way of empirically selecting between members of such a
family is thus to calculate the empirical Kendal tau (i.e. the one derived from
the observations) and then to identify the choice of parameter that reproduces
this value.
See MnKendalTauCoefficient
or MnKendalTauCoefficients
for Nematrian web functions that can be used to calculate Kendal’s tau
for a single pair of series or for multiple pairs simultaneously.