The inverse Wishart distribution
[this page | pdf | references | back links]
The inverse Wishart distribution (otherwise called the
inverted Wishart distribution) 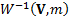 is a probability
distribution that is used in the Bayesian analysis of real-valued positive
definite matrices (e.g. matrices of the type that arise in risk management
contexts). It is a conjugate prior for the covariance matrix of a multivariate
normal distribution.
is a probability
distribution that is used in the Bayesian analysis of real-valued positive
definite matrices (e.g. matrices of the type that arise in risk management
contexts). It is a conjugate prior for the covariance matrix of a multivariate
normal distribution.
It has the following characteristics, where 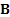 is a
is a 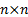 matrix,
matrix,
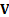 is a positive
definite matrix and
is a positive
definite matrix and 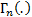 is the multivariate
gamma function.
is the multivariate
gamma function.
|
Parameters (and constraints on parameters):
|
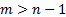 ( (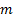 =
degrees of freedom, real) =
degrees of freedom, real)
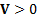 ( (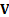 = inverse scale
matrix, positive definite) = inverse scale
matrix, positive definite)
|
|
Support (i.e. values that it can take)
|
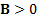 , i.e. is positive
definite, , i.e. is positive
definite, 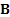 an an 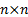 matrix matrix
|
|
Probability density function
|
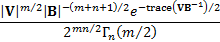
|
|
Mean
|
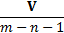
|
If the elements of 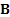 are
are 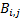 and the elements of
and the elements of
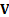 are
are 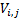 then
then
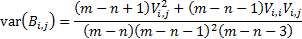
The main use of the inverse Wishart distribution appears to
arise in Bayesian statistics. Suppose we want to make an inference about a
covariance matrix, 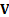 , whose prior
, whose prior 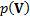 has a
has a 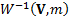 distribution. If
the observation set
distribution. If
the observation set 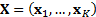 where the
where the 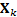 are independent
are independent 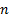 -variate
Normal (i.e. Gaussian) random variables drawn from a
-variate
Normal (i.e. Gaussian) random variables drawn from a 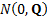 distribution then
the conditional distribution
distribution then
the conditional distribution 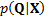 , i.e. the
probability of
, i.e. the
probability of 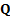 given
given 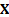 , has a
, has a 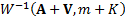 distribution, where
distribution, where
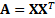 is the sample
covariance matrix.
is the sample
covariance matrix.
The univariate special case of the inverse Wishart
distribution is the inverse gamma
distribution. With 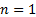 ,
, 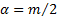 ,
, 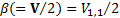 ,
, 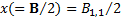 we have:
we have:
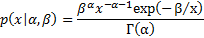
where 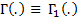 is the ordinary
(i.e. univariate) Gamma function, see MnGamma.
is the ordinary
(i.e. univariate) Gamma function, see MnGamma.
For other probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next