Blending Independent Components and
Principal Components Analysis
4.1 Similarities between PCA and ICA
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next page
4.1 Similarities
between PCA and ICA
Despite the different scale properties of PCA and ICA there
are actually many similarities. In particular, we note that the value of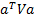 
for any
arbitrary mixture of output signals 
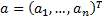of unit
length, i.e. where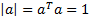 
is somewhere
between the largest eigenvector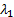 
and the
smallest one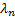 
(if the
eigenvalues are ordered appropriately) and takes its largest value when 
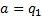. Moreover, if
we remove the signal corresponding to the largest eigenvalue using Gram-Schmidt
orthogonalisation then the remaining vector space is spanned by the remaining
eigenvectors (all of which are orthogonal to the eigenvector being removed).
Thus PCA can be re-expressed as an example of a projection
pursuit methodology but using as the importance criterion the contribution of
the input signal to aggregate output signal ensemble variance rather than the
magnitude of the input signal kurtosis. This explains the close analogy between
methods for deciding when to stop a projection pursuit algorithm and when to
truncate a PCA, i.e. random matrix theory. The two involve the same underlying
mathematics, but applied to different importance criteria.
This suggests that we can blend PCA and ICA together to
better capture the strengths of each, by adopting a projection pursuit type
methodology applied to an importance criterion that blends together variance as
well as some suitable measure(s) of independence, non-Normality and/or lack of
complexity.
NAVIGATION LINKS
Contents | Prev | Next