The gamma distribution
[this page | pdf | references | back links]
The gamma distribution is a two-parameter family of
continuous probability distributions. Two different parameterisations are in
common use, see below, with the 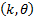 parameterisation
being apparently somewhat more common in econometrics and the
parameterisation
being apparently somewhat more common in econometrics and the 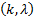 parameterisation
being somewhat more common in Bayesian statistics.
parameterisation
being somewhat more common in Bayesian statistics.
![[SmartChart]](I/GammaDistribution_files/image003.gif)
![[SmartChart]](I/GammaDistribution_files/image004.gif)
![[SmartChart]](I/GammaDistribution_files/image005.gif)
|
Distribution name
|
Gamma
distribution
|
|
Common notation
|
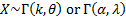
|
|
Parameters
|
Has two commonly
used parameterisations:
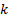 = shape
parameter ( = shape
parameter (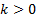 ) )
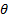 = scale
parameter ( = scale
parameter (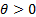 )
or )
or 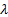 = inverse scale (i.e.
rate) parameter ( = inverse scale (i.e.
rate) parameter (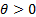 )
where )
where 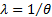 . .
Unless otherwise
specified the material below assumes the first parameterisation (i.e. using a
scale parameter)
|
|
Domain
|
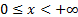
|
|
Probability density
function
|
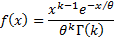
|
|
Cumulative distribution
function
|
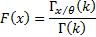
|
|
Mean
|
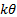
|
|
Variance
|
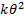
|
|
Skewness
|
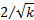
|
|
(Excess) kurtosis
|
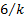
|
|
Moment generating function
|
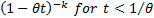
|
|
Characteristic function
|
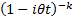
|
|
Other comments
|
The gamma distribution can also be defined with a location
parameter, 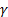 , say, in which case its
domain is shifted to , say, in which case its
domain is shifted to 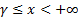 . .
Its mode is 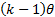 for for
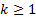 . .
If 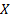 follows an exponential
distribution with rate parameter follows an exponential
distribution with rate parameter 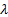 then then
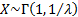 . .
If 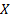 follows a chi-squared
distribution, with follows a chi-squared
distribution, with 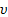 degrees of freedom, i.e.
i.e. degrees of freedom, i.e.
i.e. 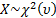 then
then 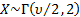 and and
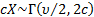 . .
If 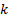 is integral then is integral then 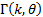 is
also called the Erlang distribution. It is the distribution of the sum
of is
also called the Erlang distribution. It is the distribution of the sum
of 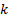 independent exponential
variables each with mean independent exponential
variables each with mean 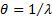 .
Events that occur independently with some average rate are commonly modelled
using a Poisson process. The waiting times between .
Events that occur independently with some average rate are commonly modelled
using a Poisson process. The waiting times between 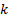 occurrences
of the event are then Erlang distributed whilst the number of events in a
given amount of time is Poisson
distributed. occurrences
of the event are then Erlang distributed whilst the number of events in a
given amount of time is Poisson
distributed.
If 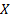 follows a Maxwell-Boltzmann
distribution with parameter follows a Maxwell-Boltzmann
distribution with parameter 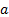 then then 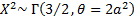 .
If .
If  follows a skew logistic
distribution with parameter follows a skew logistic
distribution with parameter 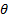 then then 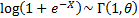 . .
The gamma distribution is the conjugate prior for the
precision (i.e. inverse variance) of a normal
distribution and for the exponential
distribution.
The gamma distribution has the ‘summation’ property that
if 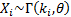 for for
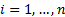 and
the and
the 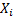 are
independent then are
independent then 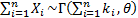 . .
Its non-central moments (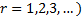 are are 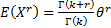 .
There is in general no simple closed form for its median. .
There is in general no simple closed form for its median.
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “gamma”.
Functions relating to a generalised version of this distribution including an
additional location (i.e. shift) parameter may be accessed by using a DistributionName
of “gamma3”, see also including
additional shift and scale parameters. For details of other supported
probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next