Extreme Events – Specimen Question
A.5.2(b) – Answer/Hints
[this page | pdf | references | back links]
Return
to Question
Q. Suppose that she is just
about to adjust her portfolio mix so that it includes no holding in A3 and with
the amounts that were invested in A3 in the above table redistributed equally
between the remaining four asset categories. What return assumptions might she
be adopting when choosing her new portfolio mix? Can you specify mathematically
all possible sets of return assumptions she could have adopted and still
reached this answer?
A similar approach as used in Question
A.5.2(a) can be used here, but with 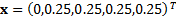 rather
than
rather
than 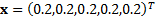 and with
one further important difference. This is that it is impossible to identify
precisely the magnitude of the implied alpha for the first asset class relative
to the others – we merely know that it is worse than a certain value, since the
no short-selling constraint (
and with
one further important difference. This is that it is impossible to identify
precisely the magnitude of the implied alpha for the first asset class relative
to the others – we merely know that it is worse than a certain value, since the
no short-selling constraint (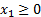 applies
to it.
applies
to it.
To solve this question we therefore need to select a very
negative return for 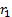 and find
implied alphas for
and find
implied alphas for 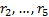 as if we
only had a 4 asset problem. We would then carry out optimisation exercises
using these values for
as if we
only had a 4 asset problem. We would then carry out optimisation exercises
using these values for 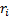 but
selectively increasing
but
selectively increasing 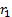 until
until 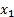 just
starts to become positive for the chosen value of
just
starts to become positive for the chosen value of 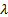 .
This has introduced a further parameter in the specification of possible asset
mixes, but one that is constrained to fall below a given value.
.
This has introduced a further parameter in the specification of possible asset
mixes, but one that is constrained to fall below a given value.
N.B. Conceptually the same sort of approach can be used if
we have more than one inequality biting although the trial and error approach
used above would soon become relatively impractical.
NAVIGATION LINKS
Contents | Prev | Next | Question