The exponential distribution
[this page | pdf | back links]
The exponential distribution describes the time between
events if these events follow a Poisson process (i.e. a stochastic process in
which events occur continuously and independently of one another). It is also
called the negative exponential distribution. It is not the same as the
exponential family of distributions.
![[SmartChart]](I/ExponentialDistribution_files/image001.gif)
![[SmartChart]](I/ExponentialDistribution_files/image002.gif)
![[SmartChart]](I/ExponentialDistribution_files/image003.gif)
|
Distribution name
|
Exponential
distribution
|
|
Common notation
|
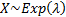
|
|
Parameters
|
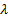 =
inverse scale (i.e. rate) parameter ( =
inverse scale (i.e. rate) parameter (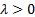 ) )
|
|
Domain
|
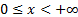
|
|
Probability density
function
|
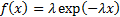
|
|
Cumulative distribution
function
|
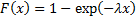
|
|
Mean
|

|
|
Variance
|
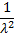
|
|
Skewness
|
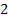
|
|
(Excess) kurtosis
|
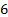
|
|
Characteristic function
|
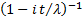
|
|
Other comments
|
The exponential distribution is a special case of the Gamma distribution,
as if 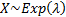 then then 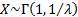 . .
The mode of an exponential distribution is 0. The quantile
function, i.e. the inverse cumulative distribution function, is 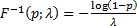 . .
The non-central moments (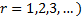 are are
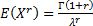 . Its median is . Its median is 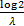 . .
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “exponential”.
Functions relating to a generalised version of this distribution including an
additional location (i.e. shift) parameter may be accessed by using a DistributionName
of “exponential2” ”, see also including
additional shift and scale parameters. For details of other supported probability
distributions see here.
NAVIGATION LINKS
Contents | Prev | Next