Deriving the principal components of two
uncorrelated return series
[this page | pdf | back links]
Suppose the returns on two uncorrelated series are 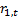 and
and
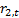 .
It is assumed that we want an analytical solution rather than a numerical
solution (a numerical solution can be found using Nematrian web services
functions that target principal components, i.e. MnPrincipalComponents,
MnPrincipalComponentsSizes
and MnPrincipalComponentsWeights).
.
It is assumed that we want an analytical solution rather than a numerical
solution (a numerical solution can be found using Nematrian web services
functions that target principal components, i.e. MnPrincipalComponents,
MnPrincipalComponentsSizes
and MnPrincipalComponentsWeights).
For a two series problem, if the covariance matrix is 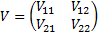 then
the principal components are associated with the eigenvectors and eigenvalues
of the covariance matrix, i.e. with values of
then
the principal components are associated with the eigenvectors and eigenvalues
of the covariance matrix, i.e. with values of 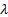 that
satisfy, for some vector
that
satisfy, for some vector 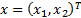 the
equation
the
equation 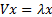 .
The
.
The 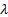 therefore
satisfy the following equations:
therefore
satisfy the following equations:
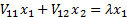
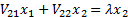
This means that 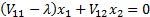 and
and
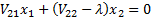 ,
i.e. (since
,
i.e. (since 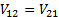 for
a covariance matrix):
for
a covariance matrix):
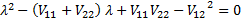
In this instance, the two series are uncorrelated and therefore
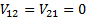 .
The quadratic then becomes
.
The quadratic then becomes 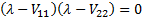 ,
i.e.
,
i.e. 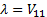 or
or
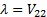 .
The (population) covariance matrix is
.
The (population) covariance matrix is 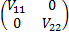 ,
which thus has two eigenvalues
,
which thus has two eigenvalues 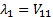 and
and
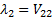 and
associated eigenvectors which are of the form
and
associated eigenvectors which are of the form 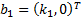 and
and
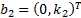 respectively
for arbitrary
respectively
for arbitrary 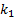 and
and
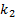 .
The first principal component is associated with whichever of
.
The first principal component is associated with whichever of 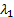 and
and
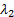 is
the larger, and the second principal component with the other one.
is
the larger, and the second principal component with the other one.
If we want principal components that are orthonormal return
series and portfolio exposures that correspond to these principal components
then the portfolio exposures must have 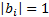 for
for
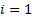 and
2, which means in this instance that
and
2, which means in this instance that 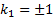 and
and
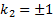 .
If we choose
.
If we choose 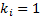 then
the resulting return series are merely de-meaned versions of the original
series, i.e. are are
then
the resulting return series are merely de-meaned versions of the original
series, i.e. are are 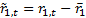 and
and
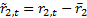 or
vice-versa depending on whether
or
vice-versa depending on whether 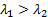 or
or
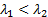 .
.