Enterprise Risk Management Formula Book
2. Series expansions (for real-valued
functions)
[this page | pdf | back links]
2.1 Exponential function and natural
logarithm (log)
function
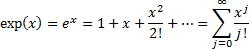
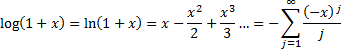
2.2 Binomial expansion
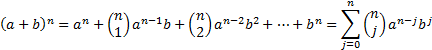
where 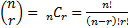 is the binomial coefficient.
is the binomial coefficient.
If we substitute into the binomial expansion 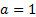 ,
,
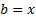 and
and 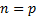 we
have (converges for any
we
have (converges for any 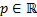 if
if 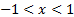 ):
):
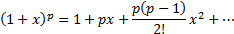
A corollary is that:
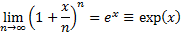
2.3 Taylor series expansion
For one variable: if series converges (where 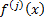 is the
is the 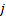 ’th
derivative of
’th
derivative of 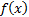 and
and 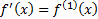 ,
, 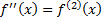 etc.):
etc.):
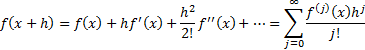
For more than one variable: e.g. for two variables,
if series converges (where 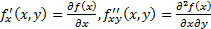 etc.):
etc.):
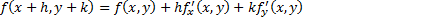
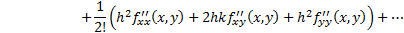
NAVIGATION LINKS
Contents | Prev | Next