Enterprise Risk Management Formula Book
Appendix A.1: Probability Distributions:
Discrete (univariate) distributions
[this page | pdf | back links]
A.1 Discrete (univariate) distributions:
Binomial (and Bernoulli), Poisson
|
Distribution name
|
Binomial
distribution
|
|
Common notation
|
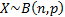
|
|
Parameters
|
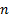 = number of
(independent) trials, positive integer = number of
(independent) trials, positive integer
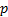 = probability
of success in each trial, = probability
of success in each trial, 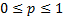
|
|
Support
|

|
|
Probability mass
function
|
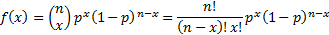
|
|
Cumulative distribution
function
|
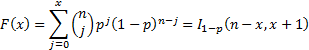
|
|
Mean
|
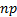
|
|
Variance
|
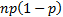
|
|
Skewness
|
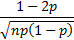
|
|
(Excess) kurtosis
|
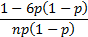
|
|
Characteristic function
|
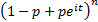
|
|
Other comments
|
Corresponds to the number of successes in a sequence of 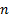 independent
experiments each of which has a probability independent
experiments each of which has a probability 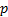 of
being successful. of
being successful.
The Bernoulli distribution is 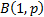 and
corresponds to the likelihood of success of a single experiment. Its
probability mass function and cumulative distribution function are: and
corresponds to the likelihood of success of a single experiment. Its
probability mass function and cumulative distribution function are:
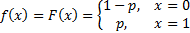
The Bernoulli distribution with 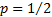 , i.e. , i.e. 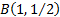 , has the
minimum possible excess kurtosis, i.e. , has the
minimum possible excess kurtosis, i.e. 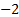 . .
The mode of 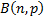 is is 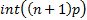 if if 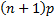 is 0 or not
an integer and is is 0 or not
an integer and is 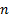 if if 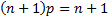 . If . If 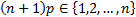 then the
distribution is bi-modal, with modes then the
distribution is bi-modal, with modes 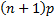 and and 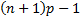 . .
|
|
Distribution name
|
Poisson distribution
|
|
Common notation
|
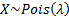
|
|
Parameters
|
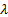 = event rate
( = event rate
(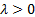 ) )
|
|
Support
|
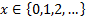
|
|
Probability mass
function
|
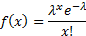
|
|
Cumulative distribution
function
|
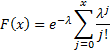
(can also be expressed using the incomplete gamma
function)
|
|
Mean
|
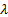
|
|
Variance
|
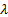
|
|
Skewness
|
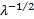
|
|
(Excess) kurtosis
|
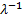
|
|
Characteristic function
|
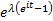
|
|
Other comments
|
Expresses the probability of a given number of events
occurring in a fixed interval of time if the events occur with a known
average rate and independently of the time since the last event.
The median is approximately 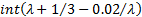 . .
The mode is 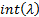 if if 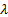 is
not integral. Otherwise the distribution is bi-modal with modes is
not integral. Otherwise the distribution is bi-modal with modes 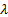 and and
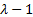 . .
|
NAVIGATION LINKS
Contents | Prev | Next