Constrained Quadratic Optimisation: 6.
Portfolio optimisation
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next
page
6. Portfolio
optimisation
In a (mean-variance) portfolio optimisation context, the
objective that we typically want to maximise is the following (or some
monotonic equivalent):
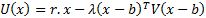
Here 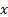 are the
portfolio weights (so typically we impose at least the following constraint
are the
portfolio weights (so typically we impose at least the following constraint 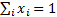 ),
), 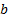 is
the benchmark (or ‘minimum risk’ portfolio),
is
the benchmark (or ‘minimum risk’ portfolio), 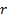 is
a vector of assumed returns on each asset and
is
a vector of assumed returns on each asset and 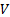 is
the covariance matrix (
is
the covariance matrix (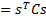 , where
, where 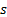 is
the vector of risks on each asset class, here assumed to be characterised by their
volatilities, as this approach is merely a mean-variance one, and
is
the vector of risks on each asset class, here assumed to be characterised by their
volatilities, as this approach is merely a mean-variance one, and 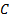 their
correlation matrix).
their
correlation matrix).
NAVIGATION LINKS
Contents | Prev | Next