Calibrating probability distributions
used for risk measurement purposes to market-implied data: 2. Multi-instrument
calibration – Section Analysis
[this page | pdf | references | back links]
Return
to Abstract and Contents
Next
Page
2.3 A multivariate normal distribution 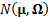 with
mean
with
mean 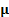 (a
vector of random variables) and covariance matrix
(a
vector of random variables) and covariance matrix 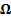 has a
probability density function,
has a
probability density function, 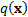 as
follows, where
as
follows, where 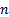 is the
number of entries in the vector
is the
number of entries in the vector 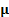 and
and 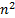 the
number of entries in
the
number of entries in 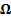 ):
):
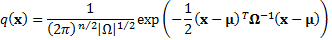
2.4 We note that:
(a) Any 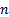 -dimensional
multivariate normal distribution has a probability density function expressible
as
-dimensional
multivariate normal distribution has a probability density function expressible
as 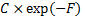 where
where 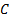 is some
suitable constant and
is some
suitable constant and 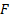 is a
positive definite symmetric quadratic form (with possibly non-zero drift) in
is a
positive definite symmetric quadratic form (with possibly non-zero drift) in 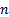 different
variables, and vice versa.
different
variables, and vice versa.
(b) Applying analytical
weighted Monte Carlo (using relative entropy) to the sort of calibration
problem referred to above will therefore return (unless the calibration problem
is ill-posed) a calibrated probability distribution which also has multivariate
normal form. This is because the problem can be restated using Lagrange multipliers
to one that involves minimising 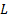 defined
as follows, where the
defined
as follows, where the 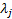 refer
to whatever calibrations there are on the means and
refer
to whatever calibrations there are on the means and 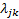 to
those on covariance terms (in general there will be fewer than
to
those on covariance terms (in general there will be fewer than 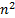 of the
of the 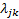 ):
):
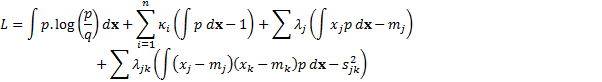
The solution to this minimisation
problem is given by the following:
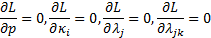
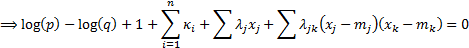
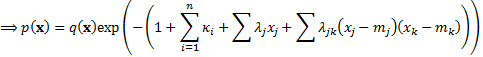
subject to 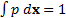 (i.e.
that
(i.e.
that 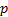 is a
probability distribution) and other constraints derived directly from
calibration requirements, e.g. that
is a
probability distribution) and other constraints derived directly from
calibration requirements, e.g. that 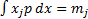 etc.
etc.
Thus if 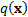 is
expressible as
is
expressible as 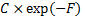 as
above, then
as
above, then 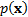 will be
too, just for a different
will be
too, just for a different 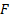 .
.
(c) Applying the
principle of no arbitrage we may therefore expect 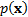 to have
zero mean (more precisely for each element of
to have
zero mean (more precisely for each element of 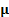 to be
the same, which without loss of generality we may take as zero if we are
focusing on relative returns) and therefore to have the form:
to be
the same, which without loss of generality we may take as zero if we are
focusing on relative returns) and therefore to have the form:
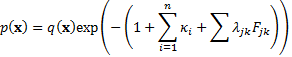
where the 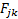 are
symmetric zero-drift quadratic forms (
are
symmetric zero-drift quadratic forms (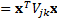 , say)
corresponding to each of the implied volatilities/implied correlations to which
we wish to calibrate.
, say)
corresponding to each of the implied volatilities/implied correlations to which
we wish to calibrate.
(d) The calibrated
distribution will therefore be multivariate normal with zero mean and
probability distribution as follows, for suitably chosen 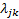 that
reproduce for the calibrations the relevant market implied variances or
covariances (where
that
reproduce for the calibrations the relevant market implied variances or
covariances (where 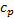 is some
constant the value of which ensures that
is some
constant the value of which ensures that 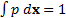 ):
):
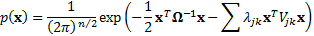
(e) Thus the calibrated
probability distribution will be characterised by a covariance matrix 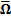 as
follows:
as
follows:
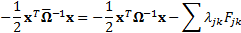
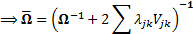
NAVIGATION LINKS
Contents | Prev | Next