Mathematical ‘Special’ Functions
[this page | pdf | back links]
Mathematicians have, over the years, developed many
different ‘special’ functions that have been found to be useful in solving
mathematical problems or evaluating physical problems. Indeed, in a sense, the
solution to ‘any’ mathematical equation can provide the opportunity to create a
new ‘special’ function, as long as a large enough body within the mathematical
community considers the solution to be sufficiently generic to be useful to
describe as a ‘special function’.
Thus, if we go back far enough in history standard
trigonometric functions like 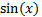 or
or 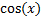 , exponential and logarithmic
functions like
, exponential and logarithmic
functions like 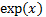 or
or 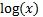 or even power functions
like
or even power functions
like 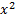 or
or 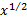 might have been viewed
as ‘special’ functions. Most of these more straightforward mathematical
functions can be evaluated using no more than the standard built-in functions
on a calculator or in a spreadsheet.
might have been viewed
as ‘special’ functions. Most of these more straightforward mathematical
functions can be evaluated using no more than the standard built-in functions
on a calculator or in a spreadsheet.
Nowadays, the term ‘special’ function is more usually
reserved for more complex mathematical functions that are relevant in several
different mathematical fields. The selection of which special functions are
sufficiently worthy to be made available directly in a mathematical function
library is thus somewhat arbitrary (and may also depend on how easy they are in
practice to compute accurately).
Typically special functions take as their inputs real
numbers, but in many cases they can also be evaluated for complex numbers. Some
special functions take single inputs, others involve more than one input.
Further details of the ‘special’ mathematical functions
supported by the Nematrian website are set out in ’special’
mathematical functions that can be evaluated using the Nematrian website.
A particular class of ‘special’ functions are polynomials
whose coefficients take specific values. Typically these are defined in the
form of series of increasingly high order polynomials that then have specified
characteristics relative to each other.