Solar-powered space flight
6b. Efficiently converting sunlight to
thrust: Advantages of proposed mirror layout over SOTV isms
[this page | pdf | references | back links]
Return to Abstract
and Contents
Next page
6.4 The two
mirror layouts proposed above are imaging and can therefore be used to provide
power (or communications) in the same manner as the mirrors proposed for the
SOTV. They also offer the following advantages over those proposed for the
SOTV:
(a) In principle
they can deliver temperatures as high as circa 5900 K, i.e. the temperature of
the sun’s photosphere (the Second Law of Thermodynamics implies that you cannot
concentrate black body radiation such as sunlight to a temperature greater than
the temperature of its source). However, this temperature exceeds the highest
melting points of any elements, which are those of tungsten, circa 3680 K, and
carbon, circa 3800 K, and so in practice it would be necessary to limit the
temperature reached to, say, circa 3700K. Operating at circa 3700 K, the
specific impulse a solar thermal engine could provide, using hydrogen as
propellant, rises to about 1000 seconds (equivalent to a propellant ejection
speed of about 10,000 ms-1). By ‘operating at circa 3700K’ we mean
that the propellant is heated to this temperature in what would otherwise in a
conventional chemical rocket be its combustion chamber. It is assumed that the
expelled propellant would then pass through a rocket throat (in much the same
manner as gasses expelled by a conventional rocket engine do), and would then
experience the same sort of adiabatic cooling traversing the rocket nozzle as
happens in a conventional rocket engine.
(b) They would reduce the
area onto which the sunlight is concentrated, which reduces the amount
reradiated away and improves overall energy efficiency. In the vicinity of the
earth, the proposed mirror layouts would concentrate sunlight onto a circle
with a radius circa 215 times smaller than the overall collector radius (and
hence circa 46,000 times smaller in area). When operating at 3700 K
approximately 15% of the incident sunlight falling onto such a solar thermal
engine would then be reradiated away. If, say, the propellant from a solar
thermal rocket left the rocket nozzle at a temperature of 1000 K then the
thermodynamic efficiency of the engine would be subject to a thermodynamic
upper limit of around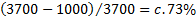 
, but it would seem
unlikely that the net conversion efficiency of the energy in the sunlight to
thrust would exceed say 40%, taking into account other potential energy losses
(although see later). For comparison, the combusted fuel in the Space Shuttle’s
main booster engine apparently reaches a temperature of at least 2000K in its
combustion chamber, but leaves the end of its rocket nozzle at c. 900K.
Parabolic mirrors can only concentrate to circa one-quarter of this
thermodynamic upper limit, see Winston (1991),
and hence to about a 30% lower temperature (although in combination with
further lenses they can get closer to the thermodynamic upper limit). This
would still mean that they would be subject to the same circa 3700K limit
referred to above; the main difference therefore is that their collector
surface area would be larger, making them less efficient overall.
(c) They can be
reused post reaching (high) orbit as a solar sail, see Kemp (2003),
either by:
-
No longer having the sun’s rays parallel to the axis of symmetry, so that
the larger mirror no longer focuses the sunlight onto the smaller mirror but
deflects it in a different direction as per a traditional single mirror solar
sail, or
-
By keeping the sun’s rays parallel to the axis of symmetry of the
vehicle, but then putting a third small mirror at the focal point of the
arrangement (instead of the solar thermal engine) and using that third mirror
to deflect the sunlight in the direction as desired as per (a). This third
mirror might most conveniently be parabolic, as then if it is suitably
positioned the deflected rays would be deflected in tolerably similar
directions, even though they would be approaching the focal point from a wide
range of angles. This approach is more complex than a traditional single mirror
solar sail, but should in principle be modestly more efficient per unit mirror
mass, see Kemp
(2003). However, it may be difficult to maintain the positioning with
sufficient accuracy, see later.
Reaching a high orbit
before switching to a solar sail is necessary because even at an altitude of,
say, 500 km atmospheric drag is still significant in the context of the very
small thrust that a solar sail might provide.
6.5 If we assume
a 40% conversion efficiency of solar power into thrust and a mirror surface
area factor of 1.1 then the mirror masses per unit lifted mass rise by a factor
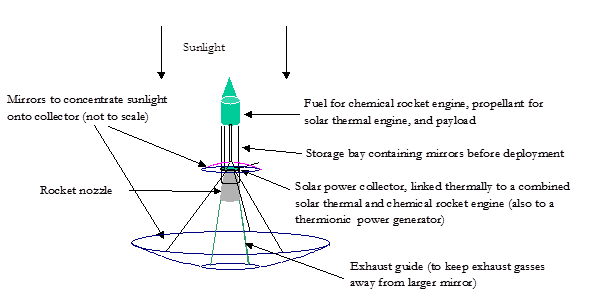
of around 3. A schematic diagram of such a vehicle, not drawn to scale, is set
out in Figure 11 (the same diagram could apply in solar sail mode as per (c)(i)
but with the sun’s rays now no longer parallel to the axis of symmetry). Please
note that there might in practice be more than three wires connecting the main
mirror to the rest of the vehicle superstructure, see later.
Figure 11. Schematic
drawing of mirror layout used for solar thermal propulsion
6.6 One worry
might be that it would be impossible to create a slab of low enough mass able
to cope with the relevant heat transfer involved with a solar thermal engine.
Careful design is likely to be needed to maximise heat transfer whilst
minimising mass and maximising structural rigidity, but it should not be
impossible. The solar power concentrated onto the slab would be approximately
46,000 × 1.37 kW m-2 = 63 × 106 kW m-2. If we assume the
slab is made of tungsten and it has a thermal conductivity of circa 100 W m-1K-1
at the relevant temperature (Kaye and Laby (1986)
have a figure of 119 at 973 K, but reducing as temperature rises) and heat
transference takes place through a slab with effective thickness for this
purpose of 1mm then the temperature differential involved would be 630K.
Tungsten has a tensile strength of 1500 – 3500 MPa. Even if all of the force
from the rocket thrust is borne by the slab, the pressure should in theory (for
the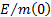 
= 10 kW/kg case
considered in Table 4) be only at most around roughly (1 + 6.2) × 
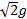× 46000 × 1.37 × 103
/ 72 = 89 MPa. As the density of tungsten is approximately 19 × 103
kg m-3, such a slab should also contribute a mass per unit mirror
area perpendicular to the sun’s rays of around 19 × 103 × 0.001 /
46000 = 0.4 g m-2. This is not an excessive amount in relation to
the probable mirror mass of, say, 5 g m-2. However, it is worth
noting that unpublished estimates that the author has seen suggest that current
solar thermal engine designs are considerably more massive than implied by this
theoretical analysis, indeed they are probably even less close to what is
theoretically achievable than are current concentrator designs, see next
section.
NAVIGATION LINKS
Contents | Prev | Next