Nematrian Website Pages on Quantum
Mechanics
[this page | pdf | references | back links]
Quantum field theory (QFT), the synthesis of quantum
mechanics and special relativity, is one of the great achievements of modern
physics. It, together with General Relativity, forms the cornerstone of the
so-called ‘Standard Model’, i.e. the current scientific understanding of how
the universe operates. Many texts explore it in further detail, including
Michele Maggiore’s ‘A Modern
Introduction to Quantum Field Theory’.
An interesting analogy with modern finance arises from the
so-called path integral formulation of quantum mechanics. This
formulation is needed to handle some elements of QFT not well handled by other
formulations, e.g. non-perturbative elements. In it we calculate the transition
probability of a movement from one state to another occurring as the sum over
all possible paths which satisfy specified boundary conditions, weighting each
path by 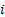 times its ‘action’ in units of
times its ‘action’ in units of 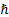 . ‘Classical’
mechanics, i.e. the position that rules in the absence of quantum mechanical
effects is recovered in a formal sense in the limit as
. ‘Classical’
mechanics, i.e. the position that rules in the absence of quantum mechanical
effects is recovered in a formal sense in the limit as 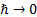 .
.
An analogy between this formulation of quantum mechanics and
derivative pricing theory is mentioned in Malcolm Kemp’s book on Market Consistency.
He notes that the ‘market’ price/value of a contingent claim can also be
derived by calculating a suitably weighted sum of all of possible paths that
the world might take that result in a given outcome.
References
Maggiore, M. (2005).
A Modern Introduction to Quantum Field Theory. Oxford University Press