Blending Independent Components and
Principal Components Analysis
3.2 Weighting schemas
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next page
3.2 Weighting schemas
There are certain types of problem where it is particularly
desirable to ascribe different levels of ‘importance’ to different input
signals according to their contribution to aggregate variability in the output
signal ensemble.
A good example is portfolio risk measurement. We might
characterise the return series coming from each individual stock as an output
series and we might be seeking a parsimonious way of explaining the variability
across the stock universe by assuming that there are a relatively modest number
of underlying factors driving the behaviour of multiple stocks, together with
some residual idiosyncratic risk factors applicable to each stock in isolation.
The ultimate aim is to estimate some measure of the likely spread of returns
that might arise from one particular portfolio (the actual portfolio chosen by
the fund manager) relative to those on a benchmark portfolio (also drawn from
the same universe but with the stocks differently weighted). A common proxy for
spread here might be the standard deviation (or variance) of the relative
return. However, this may not be a good proxy for fat-tailed distributions.
Commercial statistical factor risk models typically derive
estimates of these underlying factor signals using principal components
analysis. Suitably averaged across possible portfolios that might be chosen,
the factors exhibiting the highest eigenvalues really are the ‘most important’
ones, because they explain the most variability across the universe as a whole,
see Section
3.1. At least they do if variability and standard deviation/variance are
equated as would the case for normally distributed random variables, but not
necessarily for fat-tailed distributions. For these types of distributions,
some refinement may be desirable, see Section 4.
Implicit in PCA is thus a weighting schema being applied to
the different output signals. Suppose we multiply each individual output signal
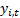 by a different
weighting factor,
by a different
weighting factor, 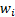 , i.e. we now
recast the problem as if the output signals were
, i.e. we now
recast the problem as if the output signals were 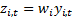 . This does
not, in some sense, alter the available information we have to identify input
signals. But what it does do is alter how much variability each given output
series contributes to the total. It will therefore alter the coefficients
defining the eigenvectors and which ones are deemed most important. Hence the
results of PCA are not scale invariant in relation to individual stocks,
since one of the implicit assumptions we are adopting is that a given quantum
of output from any given signal has the same intrinsic ‘importance’ (in
variability terms) as the same quantum of output from any other signal.
. This does
not, in some sense, alter the available information we have to identify input
signals. But what it does do is alter how much variability each given output
series contributes to the total. It will therefore alter the coefficients
defining the eigenvectors and which ones are deemed most important. Hence the
results of PCA are not scale invariant in relation to individual stocks,
since one of the implicit assumptions we are adopting is that a given quantum
of output from any given signal has the same intrinsic ‘importance’ (in
variability terms) as the same quantum of output from any other signal.
How does this compare with ICA? The projection pursuit
method introduced earlier (and corresponding infomax and maximum likelihood ICA
approaches) grade signal importance by reference to kurtosis, rather than by
reference to contribution to overall variability. As we noted earlier, kurtosis
is scale invariant. Thus ICA should identify ‘meaningful’ signals that
influence the ensemble of output signals (if we are correct to ascribe
‘meaning’ to signals that appear to exhibit ‘independence’, ‘non-Normality’ or
‘lack of complexity’), but it will not necessarily preferentially select ones
whose behaviours contribute significantly to the behaviour of the output
signal ensemble.
NAVIGATION LINKS
Contents | Prev | Next