Enterprise Risk Management Formula Book
Appendix A.5: Probability Distributions: Multivariate
probability distributions
[this page | pdf | back links]
Multivariate normal (i.e. Gaussian) distribution
The multivariate probability distribution 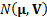 where
where 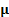 is a vector
of
is a vector
of 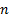 elements
and
elements
and 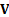 is an
is an 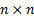 non-negative
definite matrix has the following joint density function (where
non-negative
definite matrix has the following joint density function (where 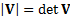 is the
determinant of V)
is the
determinant of V)
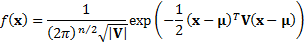
The means of the individual marginal distributions are 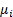 where
where 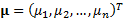 and the
covariance between the
and the
covariance between the 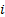 ’th and the
’th and the 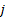 ’th
marginal distributions are
’th
marginal distributions are 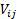 where the
where the 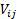 are the
elements of
are the
elements of 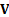 . Its moment
generating function is
. Its moment
generating function is 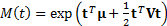 and its
characteristic function is
and its
characteristic function is 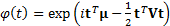 . The
multivariate normal distribution has as its copula the Gaussian copula.
. The
multivariate normal distribution has as its copula the Gaussian copula.
A bivariate random variable 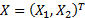 follows a standard
bivariate normal distribution if it has
follows a standard
bivariate normal distribution if it has 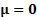 and
and 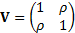 . More
generally, a multivariate normal distribution is a standard multivariate normal
distribution if
. More
generally, a multivariate normal distribution is a standard multivariate normal
distribution if 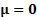 and
a covariance matrix which is also a correlation matrix, i.e. where the variance
of each individual marginal distribution is 1.
and
a covariance matrix which is also a correlation matrix, i.e. where the variance
of each individual marginal distribution is 1.
For numerical values of the cumulative distribution function
of the standard bivariate normal distribution see here.
NAVIGATION LINKS
Contents | Prev | Next